Skip to main content

Section 4.6 Tools for generating self-similar sets

Mathematically, an iterated function system is a finite collection of contractions. Now that we have a solid understanding of AffineFunction objects, we can define an IFS (on the computer) to be a list of such objects. Just an AffineFunction is an object that knows certain things about itself, we might expect an IFS to be an object that stores some relevant information. In this section we provide pointers to two Javascript based tools that implement IteratedFunctionSystems using exactly this approach.

Subsection 4.6.1 The IFS Visualizer

The IFS Visualizer provides a simple interface, implemented in a web page, that makes it pretty easy to generate images of self-similar sets. An image of the IFS Visualizer is shown in figure Figure 4.6.1 and you can find the IFS Visualizer itself at this URL: https://www.marksmath.org/visualization/IFS_Visualizer/.

Figure 4.6.1. The IFS Visualizer

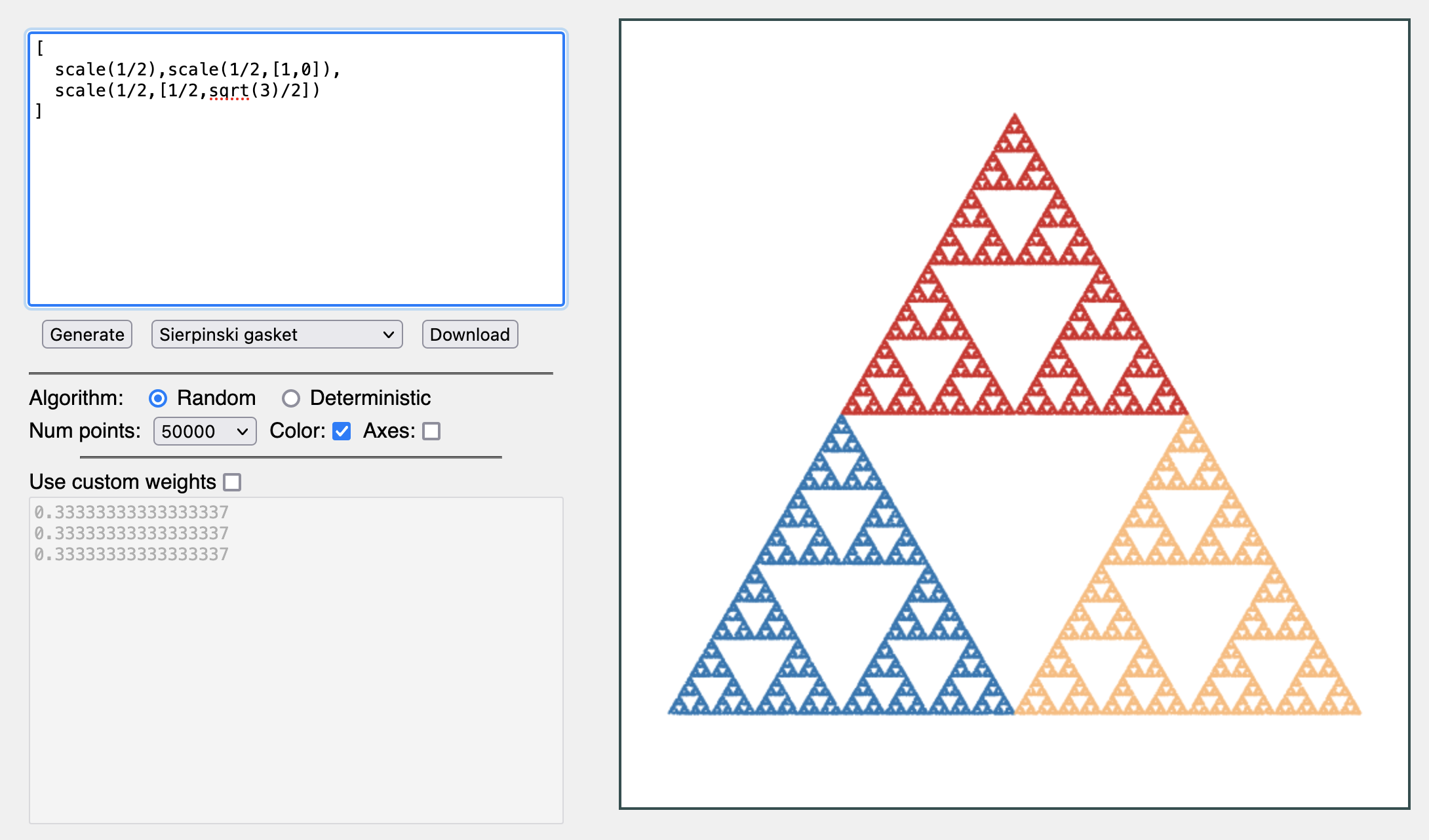
To use the IFS Visualizer, simply enter a list of AffineFunctions in the box in the upper left and hit the Generate button. There is a menu of built in examples to help get you started. The example shown in Figure 4.6.1 is the Sierpinski triangle, whose IFS is entered:

[
  scale(1/2),scale(1/2,[1,0]),
  scale(1/2,[1/2,sqrt(3)/2])
]

There are several other options that affect the way the image is drawn. We'll investigate those further as we discuss algorithms for generating self-similar sets soon.

Subsection 4.6.2 IFS tools on Observable

As conventient as the IFS Visualizer is, the lack of a full-fledged programming environment does impose some limitations. A much more feature rich programming environment can be found on Observable, which provides an online, notebook based environment for creating visualizations using Javascript. The same AffineFunction and IteratedFunctionSystem classes that power the IFS Visualizer are implemented there, which makes generating a self-similar set as easy as follows:

// Load the packages
import {
  IteratedFunctionSystem,
  scale
} from "@mcmcclur/iteratedfunctionsystem-class"

// And use them
new IteratedFunctionSystem([
  scale(0.5),
  scale(0.5, [1, 0]),
  scale(0.5, [0, 1])
]).render_stochastic({ colors: true })
Figure 4.6.2. Simple Sierpinski triangle

There's a whole lot more we can do, since we're working in a fullfledged programming environment. Figure 4.6.3, for example shows a variation on Sierpinski's theme based on a hexagon called the hexagasket.

{
  let IFS = [];
  let vertices = [];
  for (let i = 0; i & 6; i++) {
    let v = [Math.cos((i * Math.PI) / 3), Math.sin((i * Math.PI) / 3)];
    vertices.push(v);
    IFS.push(scale(1 / 3, v));
  }
  IFS = new IteratedFunctionSystem(IFS);
  return IFS.render_deterministic({
    max_depth: 4,
    init: vertices,
    fill_colors: true,
    image_width: 800
  });
}
Figure 4.6.3. The hexagasket

With these tools in hand, we'll explore many more examples and discuss the algorithms used to generate them throughout the rest of this chapter. We refer the reader who is immediately curious about aspects of software, to the following Observable notebook: https://observablehq.com/@mcmcclur/iterated-function-systems.