Section 4.7 More examples
Subsection 4.7.1 Generalized Sierpinski triangles
Any three, non-collinear points in the plane determine a triangle. If we generate an iterated function system using contractions about those points with the contraction ratio \(1/2\text{,}\) we generate a Sierpinski like construction based on the resulting triangle.
We can generate three random points and the corresponding generailized Sierpinski triangle on Observable like so:
new IteratedFunctionSystem(
d3.range(3)
.map(() => scale(1 / 2, [d3.randomUniform()(), d3.randomUniform()()]))
).render_stochastic({ colors: true })
The resulting looks a lot like Figure 4.7.1. Full code can be found in this Observable notebook: https://observablehq.com/@mcmcclur/generalized-sierpinski-triangles
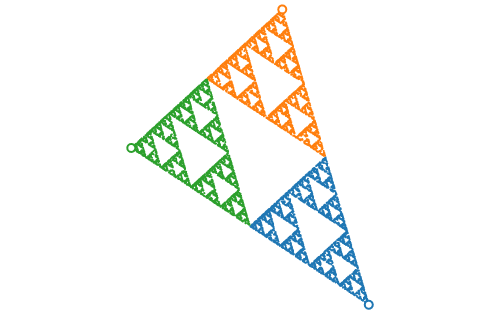
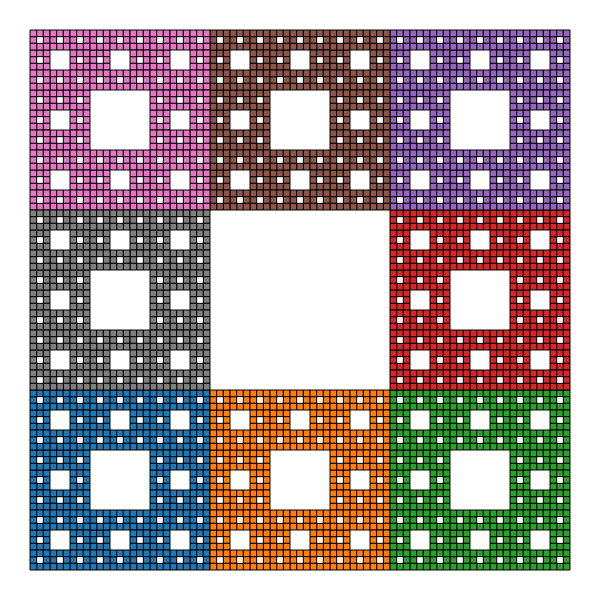
Subsection 4.7.2 The Sierpinski Carpet
The Sierpinski carpet consists of 8 copies itself scaled by the factor \(1/3\text{.}\) The IFS can be expressed used the following code:
let vertices = [
[-1, -1], [0, -1], [1, -1], [1, 0],
[1, 1], [0, 1], [-1, 1], [-1, 0]];
let carpetIFS = new IteratedFunctionSystem(
vertices.map((pt) => scale(1 / 3, pt)));
An approximation to the set is shown in Figure 4.7.2 basd on code here: https://observablehq.com/@mcmcclur/iterated-function-systems#cell-510