Iterated function systems

Section 4.3 Iterated function systems

We now provide a careful mathematical definition of one of the central tools of fractal geometry - the iterated function system or IFS. The idea behind the IFS technique is to focus on how the parts of a set might fit together to create the whole. Thus, we focus on what makes two sets similar; we do this with the notion of a similarity. An IFS is a collection of similarities and a self-similar set is the attractor of an IFS. Thus, we actually need to make several definitions, which we will illustrate with examples afterwards.

Subsection 4.3.1 IFS definitions

We assume we are working in \(\mathbb{R}^n,\) \(n\)-dimensional Euclidean space. The dimension \(n\) will almost always be \(2\) in this text, although \(n=1\) might be the natural setting for the Cantor set. Our sets will generally be subsets of the plane. Given \(x\) in \(\mathbb{R}^n,\) \(|x|\) will refer to the distance from \(x\) to the origin. Thus, \(|x-y|\) represents the distance from \(x\) to \(y.\)

Definition 4.3.1.

A function \(f:\mathbb{R}^n\to \mathbb{R}^n\) will be called a contraction if there is a real number \(r\) such that \(0<r<1\) and \(|f(x)-f(y)| \leq r|x-y|\) for all \(x,y\) in \(\mathbb{R}^n.\) If \(|f(x)-f(y)| = r|x-y|\) for all \(x,y\) in \(\mathbb{R}^n,\) then \(f\) is called a similarity and the number \(r\) is called its contraction ratio.

Definition 4.3.2.

An iterated function system on \(\mathbb{R}^n\text{,}\) or IFS, is a non-empty, finite collection of contractions of \(\mathbb{R}^n.\) We will usually express an IFS in the form

\begin{equation*} \left\{f_i\right\}_{i=1}^m, \end{equation*}

where \(m\) is the number of functions in the IFS.

We will often be interested in the case where all functions in the IFS are similarities, but that's not a requirement not is it a hypothesis in the following theorem.

Theorem 4.3.3. Existence of invariant sets.

For any IFS

\begin{equation*} \left\{f_i\right\}_{i=1}^m, \end{equation*}

there is a unique non-empty, closed, bounded subset \(E\) of \(\mathbb{R}^n\) such that

\begin{equation} E = \underset{i=1}{\overset{m}{\bigcup }}f_i(E).\label{SSEquation}\tag{4.3.1} \end{equation}

The set \(E\) defined is called the invariant set or attractor of the IFS. If the IFS consists entirely of contractive similarities, then \(E\) is called self-similar.

Subsection 4.3.2 Interpretation

We will make frequent use of Theorem 4.3.3, so let’s make sure we understand what it is saying. First, the notation \(f_i(E)\) refers to the image of the set \(E\) under the action of the function \(f_i.\) For the general function \(f:\mathbb{R}^n\to \mathbb{R}^n\) and set \(E \subset \mathbb{R}^n,\)

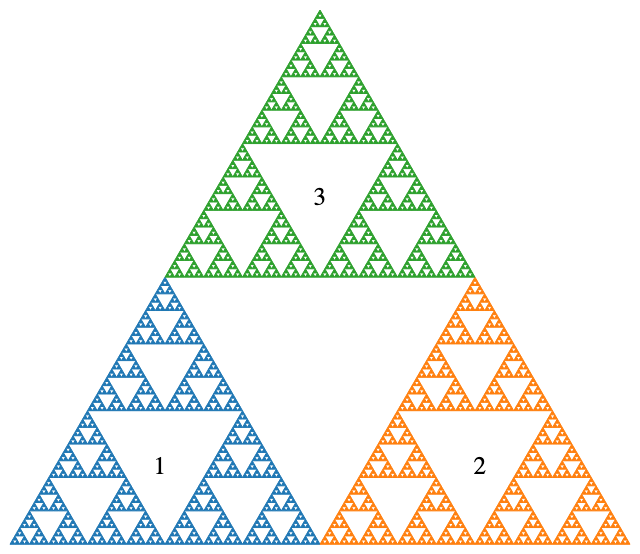
\begin{equation*} f(E)=\{f(x):x\in E\}. \end{equation*}

If the function \(f\) happens to be a similarity, then application of \(f\) transforms \(E\) into a set which is geometrically similar to \(E.\) This idea is illustrated in figure Figure 4.3.4.

Figure 4.3.4. The action of a contractive similarity on a set \(E\) in the plane

If a set is self-similar, then it can be decomposed into several parts - each of which is geometrically similar to the whole. The decomposition of the Sierpinski triangle, for example, is shown if Figure 4.3.5

Figure 4.3.5. Decomposition of the Sierpinski triangle