Section 1.2 The scope of chaos
The previous section introduced you a few fascinating ideas and images (functional iteration in real and complex variables and infinitely convoluted shapes that have become knows as fractal) - all in the context of Newton's method. The purpose of this short section is to indicate and illustrate a few other areas in which chaos and fractals occur.
Subsection 1.2.1 The iteration of real functions
We were introduced to the idea of real iteration back in Subsection 1.1.2 but there's no reason the function we iterate needs to come from Newton's method. Figure 1.2.1 illustrates iteration using a geometric cool called a cobweb plot. In part (a) we see the iteration of \(N(x)=x/2+1/x\text{,}\) that arises in Newton's method. In part (b) we the iteration of \(f(x)=3.1x(1-x)\text{.}\) This is an example of a logistic function and really has nothing directly to do with Newton's method.
The logistic function above is a member of a family of functions - the logistic family. These functions have the form \(f_r(x) = rx(1-x)\text{.}\) When studying a family of functions like this we are often interested in the various types of behavior that might arise. We can explore these possibilites with a tool called a bifurcation diagram. The bifurcation diagram for the logistic family is shown in Figure 1.2.2.
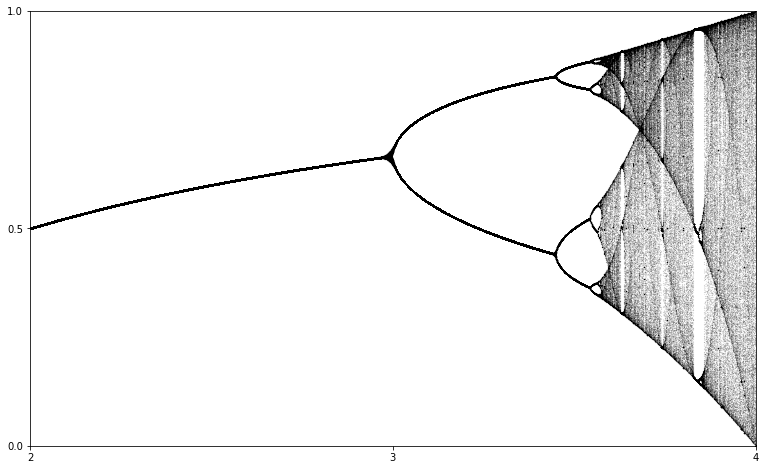
Subsection 1.2.2 The iteration of complex functions
We were introduced to the idea of complex iteration back in Subsection 1.1.3 and, again, there's no reason the function we iterate needs to come from Newton's method. In the context of complex iteration we'll meet Julia sets, a few of which are shown in Figure 1.2.3
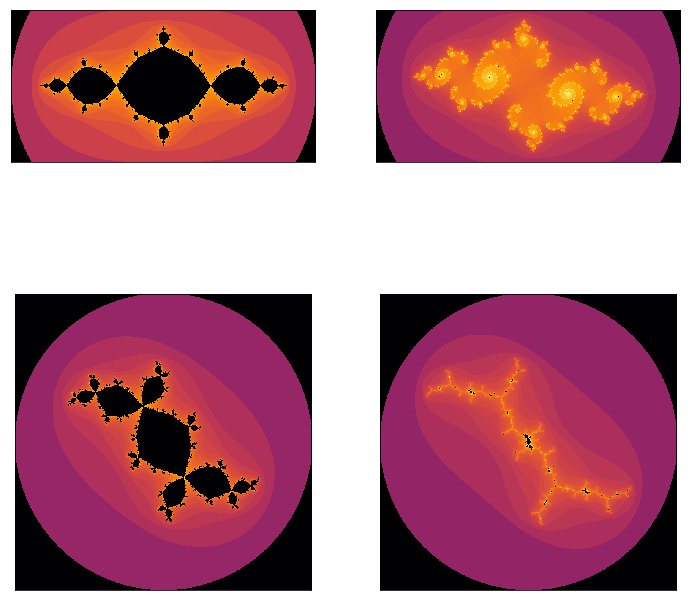
The Julia sets shown in Figure 1.2.3 all arise from the iteration of functions in the quadratic family - i.e. from the iteration of functions of the form \(f(z)=z^2+c\text{.}\) It is in this context that the famous Mandelbrot set shown in Figure 1.2.4 arises.
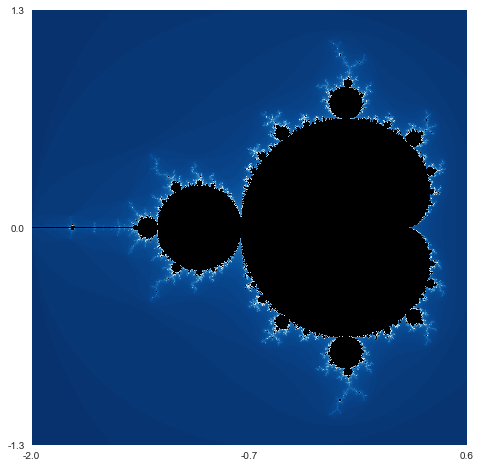
Subsection 1.2.3 Geometric iteration and fractal geometry
When studying fractal geometry, we might iterate a function that maps sets to other sets. Such an example is shown in Figure 1.2.5. The limiting figure, called the Sierpinski triangle is shown in Figure 1.2.6.

The specific type of function that we iterate in this context is called an iterated function system Some amazingly intricate images can be constructed using an iterated function system. Figure 1.2.7 shows the Barnsely fern, which is described by a list of just four functions.
