Figure Figure 5 shows that there are lots of disk-like bulbs attached to the main cardioid. As \(c\) moves from the main cardioid into one of these bulbs, \(f_c\) bifurcates from having an attractive fixed point, to an orbit of period \(q\) for some integer \(q \gt 1\text{.}\) After the period 2 bulb, the two next largest bulbs near the top and bottom of the main cardioid are period 3 bulbs. The other bulbs have larger period still.

Let's try to gain a quantitative understand of the nature of these bulbs. To do so, we re-consider our description of the main cardioid from subsection Subsection 1. Again, the interior of the main cardioid can be characterized algebraically as \begin{align} f_c(z) &= z \\ |f_c'(z)| &\lt 1. \end{align} More generally, though, we can obtain a fixed point with any given multiplier \(\gamma\) that we like by solving \begin{align} f_c(z) &= z \\ f_c'(z) &= \gamma. \end{align} If we solve this system for \(c\) and \(z\text{,}\) we obtain \begin{align} c &= \frac{1}{4} \left(2\gamma - \gamma^2\right)\\ z &= \gamma/2. \end{align} Thus, \(f_c\) has a fixed point with multiplier \(\gamma\) at \(\gamma/2\) when \(c=(2\gamma - \gamma^2)/4\text{.}\)

Let us now define \(c(\gamma) = (2\gamma - \gamma^2)/4\) and consider the image of rays of the form \(r\exp(2\pi i \theta)\text{,}\) where \(\theta\) is fixed and \(0\leq r \leq 1\text{.}\) These should all lie within the main cardioid and stretch from zero to a point on the boundary of the cardioid. Some of these are plotted in figure Figure 6.

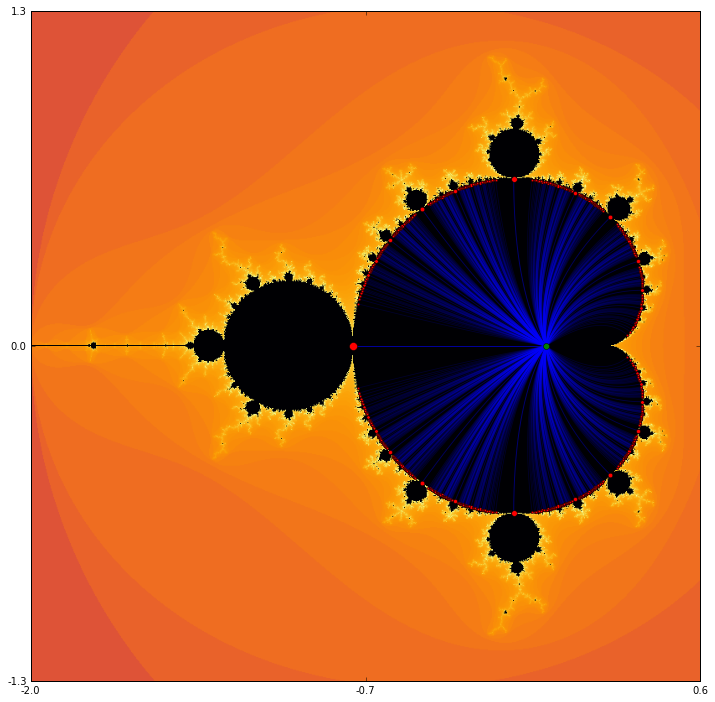
Note that the rays shown in figure Figure 6 all correspond to rational values of \(\theta\) and, as it appears, a periodic bulb is attached to the main cardioid at every rational ray. Even more is true - if \(\theta=p/q\text{,}\) then the bulb attached to the main cardioid at the point \(c(\exp(2\pi i \theta))\) has period \(q\) and rotation number \(p\text{.}\)

To understand this, recall that \(c(\gamma)\) is built specifically so that \(f_{c(\gamma)}\) will have multiplier \(\gamma\text{.}\) So, what happens to the attractive orbits of \(f_c(\gamma)\) for

for a fixed rational value of \(\theta\) as \(r\) moves from zero up to one and even just a little bit past? For \(r \lt 1\text{,}\) \(f_c\) has an attractive fixed point. For \(r=1\text{,}\) \(f_c\) has a neutral fixed point with multiplier \(\gamma=\exp(2\pi i \theta)\text{.}\) Note that the geometric effect of multiplying by this particular value of \(\gamma\) is to rotate through the angle \(2\pi\theta=2\pi p/q\text{.}\) If we do this \(q\) times, we've rotated through the angle \(2\pi\theta=2\pi p\text{,}\) which returns to where we started. We might expect an attractive orbit of period \(q\text{;}\) we don't have it yet because the origin still in the basin of the neutral fixed point. Once \(r \gt 1\text{,}\) that fixed point becomes slightly repulsive and the attractive orbit of period \(q\) appears.

Note that each of these bulbs has further bulbs sprouting off and similar considerations apply.