The dynamic behavior illustrated by the previous two examples is quite typical for the iteration of a polynomial on \(\mathbb C\text{.}\) The plane decomposes into two disjoint regions - a stable region and an unstable region. By the very characterization of stability, the stable region is an open set and the unstable region is closed. Points in the stable region converge to some attractive behavior while the behavior is chaotic on the unstable region.

The geometry of the unstable region is typically much more complicated than the geometry in the previous two examples. Let's explore the function \(f(z)=z^2-1\) experimentally to see what other types of behavior can arise.

First, let's give a little thought to the types of behavior that might arise. It seems reasonable to suspect that, if \(|z|\) is large, then any quadratic will behave something like \(z^2\text{.}\) Thus, we expect that, once an iterate is large enough, its orbit will escape to \(\infty\text{.}\) Let's try to prove this a little more rigorously. Suppose that \(|z_0| \gt 2\) and write \(|z_0|=2+\varepsilon\text{,}\) where \(\varepsilon\) must be some positive number. Then, \begin{align*} |f(z_0)| & = |z_0^2-1| \geq \left||z_0^2|-|1|\right| = |z_0|^2 - 1 \\ & \geq |z_0^2| - |z_0| = |z_0|(|z_0|-1) = |z_0|(1+\varepsilon). \end{align*} By induction, \(|f^n(z_0)| \geq |z_0|(1+\varepsilon)^n \to \infty\text{.}\) Thus, once an orbit exceeds 2 in absolute value, it must escape to \(\infty\)

On the other hand, there are certainly plenty of orbits that are bounded because, as we know, the points \(0\) and \(-1\) form a super attractive orbit of period 2. Thus, there should be a little disk about each of those points containing points that are attracted to that orbit. A reasonable question is, how close must we be to one of those points to guarantee convergence to that orbit? To address this, let

Note that \(0\) and \(-1\) are both super-attractive fixed points of \(F\text{.}\) We can be confident that an iterate \(z_k\) of \(F\) will converge to one of those fixed points if it's close to the fixed point and \(|F'(z_k)| \lt 1\text{.}\)

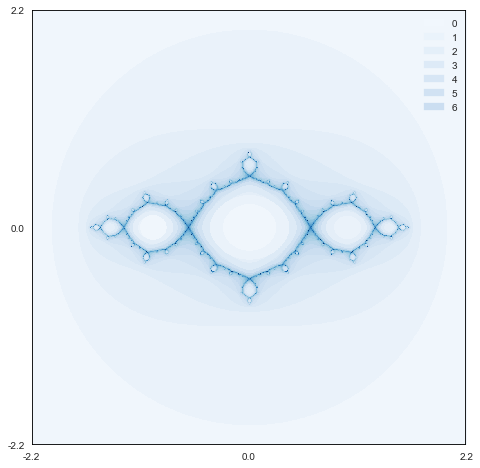
Taking all this into account, let's describe an experimental procedure to explore the dynamics of \(f\text{.}\) First, we define a rectangular region in the complex plane. Specifically, let \(R\) denote the square with lower left corner at the point \(-2.2-2.2i\) and with upper right corner \(2.2+2.2i\text{.}\) Break that square up into pixels of dimension, say, \(1000\times1000\) - each corresponding to a complex number \(z_0\text{.}\) For each of those pixels, iterate from \(z_0\) until one of three things happens.

1. The iterate \(z_k\) exceeds 2 in absolute value
2. \(|F'(z_k)| \lt 1\) and \(\text{Re}(z_k) \lt 0.618\)
3. We're tired

We then shade the result according to how many times we've iterated. The result is shown in figure Figure 1.

An interactive orbit generator for this function is included on this webpage: https://goo.gl/04o9AY.