Skip to main content
\( \newcommand{\lt}{<} \newcommand{\gt}{>} \newcommand{\amp}{&} \)

Section5.6Exercises

2

Show that the image of the circle of radius \(|c|\) centered at \(c\) under \(f_c\) is the circle of radius \(|c|^2\) centered at the origin.

In the next couple of problems, we'll try to get a grip on the family of functions \(g_{\lambda}(z) = \lambda z + z^2\text{.}\)

3

The escape radius

  1. Use the triangle inequality to show that \(|g_{\lambda}(z_0) \geq |z_0|\text{,}\) whenever \(|z_0| \gt 2\lambda\text{.}\) Conclude that the orbit of \(z_0\) escapes whenever an iterate excedes \(2\lambda\text{.}\)
  2. How does this compare to our general polynomial escape criterion?
4

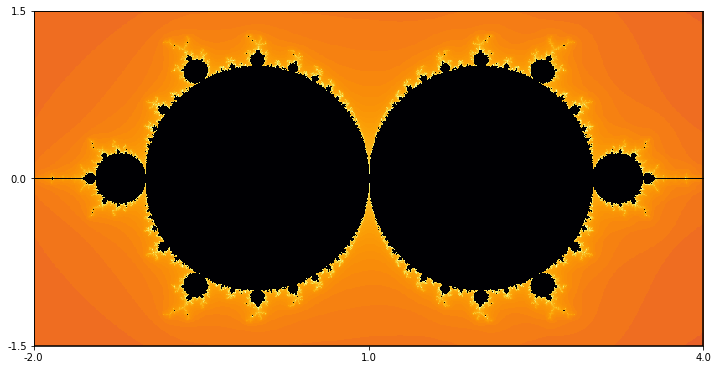
The escape locus for \(g_{\lambda}\) (or any family of quadratics) is a partition of the complex parameter plane into two regions - one where the critical orbit stays bounded and one where the critical orbit diverges. This escape locus is shown in figure Figure 7. Let's try to understand a couple of things about this image.

  1. Show that the origin is an attractive (or super-attracitve) fixed point of \(g_{\lambda}\text{,}\) whenever \(|\lambda| \lt 1\text{.}\) This observation yields what prominent feature in figure Figure 7?

  2. Let \(\varphi(z) = z + (1-\lambda)\text{.}\) Show that

    \begin{equation*} g_{\lambda} \circ \varphi = \varphi \circ g_{2-\lambda}. \end{equation*}

    How is this observation related to the symmetry that we see in figure Figure 7?

Figure5.6.7The escape locus for \(g_{\lambda}(z) = \lambda z + z^2\text{.}\)