To this point, our functions have been polynomials. Polynomials are awesome! They always have fixed points and many other periodic orbits; they always critical points; and there's always a reasonable escape criterion. As we move away from polynomials and consider other types of functions, we lose most of that. However (as we'll prove in the next chapter), the behavior of fixed and periodic points (if they exist) remains consistent.

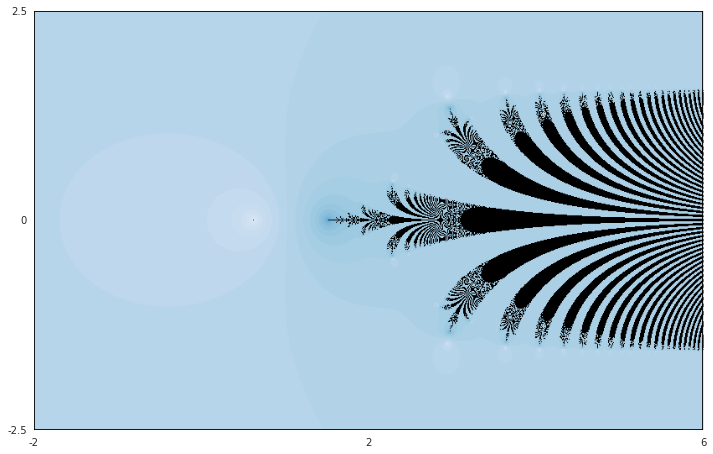
A function that is differentiable at every point in the complex plane that is not a polynomial is called an entire function. Perhaps the simplest example of such a function is the exponential function. In this section, we'll explore the dynamical behavior of \(f(z) = e^z/3\text{.}\) While plain old \(e^z\) might seem more natural, it lacks any attractive behavior. Our function \(f\) has exactly one real fixed point as a simple graph shows.

Now, to understand the dynamical behavior of \(f\text{,}\) we can choose a region containing the fixed point, decompose it into pixels, and iterate from each pixel until we are either close to the fixed point or ... something else I guess. An exponential function grows quickly for large values of \(\text{Re}(z)\text{.}\) So it might make sense to bail out for, say, \(\text{Re}(z) \gt 500\text{.}\) The result is shown in figure Figure 2.