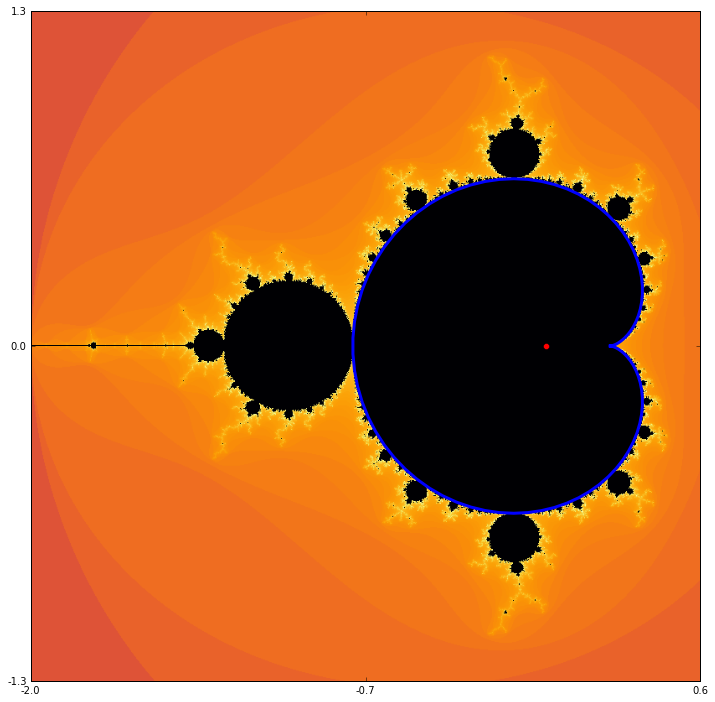
Subsection5.5.1The main cardioid
The interior of the main cardioid consists of all those values of \(c\) with the property that \(f_c\) has an attractive fixed point. This can be characterized algebraically as \begin{align} f_c(z) &= z \\ |f_c'(z)| &\lt 1. \end{align} Now, on the boundary we should have \begin{align} f_c(z) &= z \\ |f_c'(z)| &= 1. \end{align} That is, the fixed point is no longer strictly attractive on the boundary but just neutral. Since any complex number of absolute value 1 can be expressed in the form \(e^{2\pi i t}\text{,}\) this pair of equations can be written without the absolute value: \begin{align} f_c(z) &= z \\ f_c'(z) &= e^{2\pi i t}, \end{align} for some \(t\text{.}\) Taking into account the fact that \(f_c(z) = z^2+c\text{,}\) we get \begin{align} z^2+c &= z \\ 2z &= e^{2\pi i t}. \end{align} This system of equations can be solved for \(z\) and \(c\) in terms of \(t\text{.}\) It's not even particularly hard. The second equation yields \(z=e^{2\pi i t}/2\text{.}\) This can be plugged into the first equation to get
\begin{equation*} c = e^{it}/2 - e^{2it}/4. \end{equation*}This happens to be the parametric representation of a cardioid and is exactly the formula used to generate figure Figure 1