MML - Review for Exam 4

We will have our fourth exam next Wednesday, April 23. This review sheet is again meant to help you succeed on that exam.

  1. What is the sigmoid function \(\sigma(x)\)? More specifically,

    1. Write down the exact algebraic definition of \(\sigma(x)\).
    2. Draw a graph of \(\sigma(x)\).
    3. In the context of binary classification, how do we interpret the sigmoid?
    4. Show that \(\sigma(x)\) satisfies the equation \(\sigma' = \sigma(1-\sigma)\).
    5. Suppose that the number \(x_0\) is chosen so that \(\sigma(x_0) = 0.8\). Compute \(\sigma'(x_0)\).

  2. What is the ReLU function \(\text{ReLU}(x)\)? More specifically,

    1. Write down the exact algebraic definition of \(\text{ReLU}(x)\).
    2. Draw a graph of \(\text{ReLU}(x)\).
    3. Suppose that the number \(x_0\) is chosen so that \(\text{ReLU}(x) = 0.8\). Compute \(\text{ReLU}'(x)\).

  3. Let’s suppose that \(x\) and \(y\) represent two vectors of purely categorical data. Let’s say

    \[\begin{aligned} x &= [\text{red}, \text{yel}, \text{blu}, \text{blu}, \text{yel}, \text{yel}] \\ y &= [\text{blu}, \text{yel}, \text{red}, \text{blu}, \text{yel}, \text{yel}]. \end{aligned}\]

    How do you compute the Hamming distance between these two vectors and what is the value?

  4. Consider the categorical data vector \[[\text{red}, \text{yel}],\] where the set of all possible values for the each entry is red, yel, and blu. Write down the one-hot encoding of that data vector.

  5. Consider the vectors of mixed type

    \[\begin{aligned} x &= [\text{red}, \text{yel}, 8, 4] \\ y &= [\text{blu}, \text{yel}, 2, 7]. \end{aligned}\]

    Let’s suppose that the numerical variable can take values from 0 to 10.

    1. What is the standard Gower distance between these vectors?
    2. Why might we like to use the Gower distance in K Nearest Neighbor algorithms?

  6. Draw an expression graph for \[f(x_1, x_2) = x_1^2 e^{-(x_1^2 + 2 x_2^2)}.\] Be sure to reuse node values as necessary.

  7. Compute the convolution of the data \(D\) with the kernel \(K\) given by

\(D=\,\) 1 1 2 2 3 3

and

\(K=\,\) 2 0 2 .

  1. Consider the two two-dimensional kernels \[ K_1 = \begin{bmatrix}1&1&1\\1&-8&1\\1&1&1\end{bmatrix} \quad \text{ and } \quad K_2 = \begin{bmatrix}1&1&1&1&1\\1&1&1&1&1\\1&1&-24&1&1\\1&1&1&1&1\\1&1&1&1&1\end{bmatrix}. \]

    1. Could these be appropriate for edge detection in image processing? Why or why not?
    2. What kind of difference might you expect in the behavior of these?

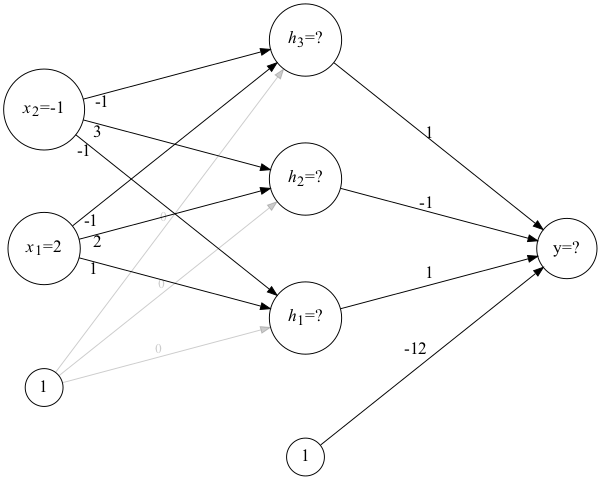
  2. The neural network shown in figure 1 below consists of three layers:

    • the input layer,
    • one hidden layer, and
    • the output layer.

    Let’s also suppose that the input layer has a ReLU activation and the output layer has a sigmoid activation.

    Note that the inputs are given. Use those inputs together with forward propagation to compute the value produced by this neural network.

A simple neural network image for computation
Figure 1: A neural network image