from sympy import pi, var, exp, sqrt, integrate
x = var('x')
integrate(exp(-x**2/2)/sqrt(2*pi), (x,-2,1))\(\displaystyle \frac{\operatorname{erf}{\left(\frac{\sqrt{2}}{2} \right)}}{2} + \frac{\operatorname{erf}{\left(\sqrt{2} \right)}}{2}\)
A survey of Calculus
Our view of Calc I
In this first, purely mathematical presentation, we’ll take a survey of the calculus that we’ll need to know for machine learning. Since Calculus I is a prerequisite for this course, I’ll assume that you’ve been at least exposed to Calculus.
In this presentation, we’ll survey that part of Calc I that you need to know from a perspective that should be relevant for machine learning.
What do you need to know?
From Calculus I, you certainly need to be familiar with the concepts of functions, derivatives, and integrals.
You shouldn’t be scared of taking the derivative of, say, \(f(x)=e^{-x^2}\). And you should know that the result \(f'(x)\) is a new function that tells you about the rate of change of the original and that you can use this to find the maximum of the function.
You should also understand the concept of the integral and that the accumulated, singed area under the of graph \(y=f(x)\) over the interval \([a,b]\) is represented by
\[\int_a^b f(x)\,dx.\]
Some things we’ll de-emphasize
Intense algebraic manipulation
We’ll do some algebra, to be sure, but not just for the sake of doing it. For example, we’ll discuss integration via \(u\)-substitution here in this presentation; we won’t get into the trickier types of integration techniques that you learn after that in Calc II.Trigonometry
We’ll use some basic trigonometry a bit when we discuss the dot product and rotation matrices. We won’t use it much beyond that, though, and won’t spend time reviewing it.Theory at a deep level
We won’t use \(\varepsilon\)s and \(\delta\)s to prove statements about limits and we won’t the mean value theorem to prove that \(f' = 0\) implies that \(f\) is constant. We will discuss theory at an intuitive level relying on geometry and computational verification.
What else will you need to know?
Calculus I covers really only just a small part of the calculus that you need to know for machine learning.
The most obvious piece that you’re missing is multivariable calculus, that you typically discuss in Calc III.
In addition, it’s important to appreciate Calculus from a numerical perspective. That is, we’ll be doing a lot of math on the computer in a way that yields numerical estimates. We need to understand how to do that and how to interpret it.
Our survey here of Calculus I will take that numerical perspective into account from the start.
Functions
In one sense, calculus could be understood as a particular bag of tricks to analyze functions.
In Calculus I, we study functions of a single variable. That is, we study functions \(f:\mathbb R \to \mathbb R\).
You should certainly be comfortable with basic functions and their graphs.
Quadratic example
A quadratic has the form \(f(x) = ax^2 + bx + c\). Its graph is a parabola opening up, if \(a>0\), its vertex lies at \(x=-b/(2a)\) and its \(y\)-intercept is at \(y=c\).
Thus, it’s not hard to to sketch the graph of these things. Of course, you can also use technology as I’ve done to create the graph of \(f(x) = \frac{1}{2}x^2 - 10x\) shown below.
Parameters
It’s particularly important for us to be able to think of functions in terms of parameters - i.e., symbols representing constant numbers that vary. The image below, for example shows the graph of \[f(x) = a(x-b)^2 + c.\]
Exponential example
Exponential functions have the form \(f(x) = b^x\) where \(b>0\). If \(b>1\), then \[\lim_{x\to\infty} b^x = \infty \text{ and } \lim_{x\to-\infty} f(x) = 0.\]
Limits
One way to think of calculus is as a particular bag of tricks with which to analyze functions.
That bag of tricks could be defined as those that depend on the notion of the limit and includes:
- Continuity,
- Differentiation, and
- Integration.
Definition
When we say that \(\lim_{x\to a} f(x) = L\), we mean that
For every \(\varepsilon>0\), there is a \(\delta>0\) such that \[|f(x)-L| < \varepsilon \text{ whenever } 0<|x-a|<\delta.\]
Or, more intuitively,
We can make the distance between \(f(x)\) and \(L\) as small as we like by taking the distance between \(x\) and \(a\) to be as small as is necessary, though not zero.
Note that \(\varepsilon\) is a quantitative measure of how small we’d like the distance between \(f(x)\) and \(L\) to be and \(\delta\) is a quantitative measure of how small we need the distance between \(x\) and \(a\) to be.
Geometric example
Here’s a dynamic image illustrating the fact that \[\lim_{x\to 2} \frac{1}{4}x(6-x) = 2.\]
Algebraic computation
Note that limits interact nicely with the algebraic operations. That is, \[ \lim_{x\to a} (f(x) + g(x)) = \lim_{x\to a} f(x) + \lim_{x\to a} g(x) \] and similarly for multiplication and subtraction. You do need to be careful with division, though.
As a result, we can compute limits involving polynomials by simply plugging in the number.
Thus,
\[\lim_{x\to 2} \frac{1}{4}x(6-x) = \frac{1}{4}\times2\times(6-2) = 2.\]
Division
A good example to keep in mind is \[\lim_{x\to1} \frac{x^2-1}{x-1} = \frac{0}{0} = ??\]
In order to deal with this, we need to simplify first to avoid the division by zero:
\[ \begin{aligned} \lim_{x\to1} \frac{x^2-1}{x-1} &= \lim_{x\to1} \frac{(x+1)(x-1)}{x-1} \\ &= \lim_{x\to1} (x+1) = 2. \end{aligned} \]
Taking care with the simplification
It’s important to understand that
\[\frac{x^2-1}{x-1} = \frac{(x+1)(x-1)}{x-1} \color{red}{\neq} x+1.\]
The distinction is that the final expression is defined at \(x=1\), while the original expression is not. Thus,
\[\frac{x^2-1}{x-1} = x+1\]
for all \(x\) except \(x=1\). That one value, though, has no bearing on the limit.
Geometric interpretation
From a geometric perspective, the graph looks like so:
Limits at \(\infty\)
We can also take limits as \(x\to\pm\infty\). For example,
\[\begin{aligned} \lim_{x\to\infty} \frac{2x^2 - 1}{x^2 + 1} &= \lim_{x\to\infty} \frac{x^2(2 - 1/x^2)}{x^2(1 + 1/x^2)} \\ &= \lim_{x\to\infty} \frac{2 - 1/x^2}{1 + 1/x^2} = \frac{2 - 0}{1 + 0} = 2. \end{aligned}\]
Note that we’ve factored out the highest order powers and canceled them to avoid getting an \(\infty/\infty\) term and, then used the fact that \[ \frac{\text{constant}}{\text{term that grows without bound}} \to 0. \]
Balancing powers
Generally, it’s easy to compute \(p(x)/q(x)\) as \(x\to\pm\infty\), when \(p\) and \(q\) are polynomials. We get
- \(p(x)/q(x) \to 0\) if \(\text{deg}(p) < \text{deg}(q)\),
- \(p(x)/q(x) \to \pm\infty\) if \(\text{deg}(p) > \text{deg}(q)\), and
- \(p(x)/q(x)\) approaches the ratio of the highest order coefficients if \(\text{deg}(p) = \text{deg}(q)\).
For example,
\[\lim_{x\to\infty} \frac{2x^2}{3x^3+1} = 0.\]
Exponential limit revisited
Finally, it’s easy to see why \[ \lim_{x\to-\infty} e^x = \lim_{x\to-\infty} \frac{1}{e^{-x}} = 0. \]
The reason is that \(e^{-x}\) grows without bound as \(x\to-\infty\).
Continuity
In the last column of slides, we saw that it’s easy to compute the limit \[ \lim_{x\to a} p(x), \] whenever \(p\) is a polynomial. You can just plug the number in! That is \[ \lim_{x\to a} p(x) = p(a). \] Functions with this property are said to be continuous at \(x=a\).
Definition
If \(f\) is defined on a domain \(D\subset \mathbb R\) and \(a\in D\), then we say that \(f\) is continuous at \(x=a\), if \[ \lim_{x\to a} f(x) = f(a). \]
If \(f\) is continuous at all points of \(D\), then we say that \(f\) is continuous on \(D\).
Note that the limit is taken over \(x\in D\). For example, the square root function is continuous at \(x=0\), since \[ \lim_{x\to0^+} \sqrt{x} = 0. \]
Non examples
- \(f(x) = 1/x\) is not continuous at \(x=0\); it’s not even defined there!
- The Heaviside function defined by \[ f(x) = \begin{cases} 0 & x < 0 \\ 1 & x \geq 0\end{cases} \] is not continuous at \(x=0\).
Aside
The Heaviside function arises as the derivative of the widely used ReLU activator function in neural networks.
Theorems
Continuous functions have nice properties that allow us to establish certain useful theorems. Specifically, these theorems allow us to prove the existence of solutions of equations. And, it’s nice to know that there is a solution before you go trying to find one!
The two most basic examples are:
- The intermediate value theorem (IVT) and
- The extreme value theorem (EVT).
The intermediate value theorem
Suppose that \(f:[a,b]\to\mathbb R\) is continuous and that \(Y\) is a number between \(f(a)\) and \(f(b)\). Then, there is a number \(c\in(a,b)\) such that \(f(c) = Y\).
I mean, it’s pretty easy to see why, once you’ve wrapped your head around the terminology. Note, though, this is not a uniqueness theorem.
The extreme value theorem
Suppose that \(f:[a,b]\to\mathbb R\) is continuous. Then, there are numbers \(c,d\in[a,b]\) such that \(f(c) \leq f(x)\) for all \(x\in[a,b]\) and \(f(d) \geq f(x)\) for all \(x\in[a,b]\).
Aside
In machine learning, we are often interested in optimizing the output of an algorithm defined in terms of parameters. These kinds of theorems are very valuable in that context, since they allow us to assert that we can expect that there is a solution under the appropriate hypotheses.
Derivatives
Given a function \(f\) defined on a domain \(D\subset \mathbb R\), the derivative, \(f'\), of \(f\) is a new function that gives you some important information about the original.
In particular, \(f'(c)\) tells you the rate of change of \(f(x)\) at the point \(c\).
Geometrically, this can be interpreted as slope. There are loads of other potential application, though.
Geometric example
In the image below, the thick, purple graph is the the graph of \(f\) and the thin, dashed, blue graph is \(f'\).
Note that the roots of \(f'\) occur at the local extremes of \(f\). When \(f'>0\), the graph of \(f\) is on the way up.
Differentiation rules
You probably remember using algebraic rules to compute derivatives of functions. For example,
- \(\frac{d}{dx} (3x^4 - 2x^2 - 1) = 12x^3 - 4x\) and
- \(\frac{d}{dx} x^2 e^x = 2x e^x + x^2 e^x\).
The first applies the power rule \(\frac{d}{dx} x^p = px^{p-1}\), together with the linear combination rule \[\frac{d}{dx} (a f(x) + b g(x)) = a f'(x) + b g'(x).\]
The second uses the exponential rule \(\frac{d}{dx} e^x = e^x\) and the product rule as well \[\frac{d}{dx} f(x)g(x) = f'(x)g(x) + f(x)g'(x).\]
The chain rule
The last rule that you typically learn is the chain rule: \[\frac{d}{dx} f(g(x)) = f'(g(x))g'(x).\]
For example, \[\frac{d}{dx} (x^2+1)^{100} = 100(x^2+1)^{99} \times 2x = 200x(x^2+1)^{99}.\]
And \[ \frac{d}{dx} e^{-x^2} = -2x e^{-x^2}. \]
The difference quotient
Ultimately, all these rules really come from the definition of the derivative stated in terms of the difference quotient:
\[f'(x) = \lim_{h\to0} \frac{f(x+h)-f(x)}{h}.\]
We will not spend time evaluating derivatives using this definition or deriving the differentiation rules.
It’s more important that we understand why this gives us the slope of the graph of the function.
Geometric interpretation
In the figure below, the purple graph is the graph of a function \(f\), the dashed, blue line is the graph of the tangent line at \(x=1\), and the thin orange line is the graph of a secant line \(x=1\) whose slope is determined by the difference quotient. You can set the value of \(h\) with the slider.
Optimization
A key application of the derivative is optimization. In the context of single variable calculus, this amounts to finding maxima and minima of functions.
Let’s suppose that \(f:[a,b]\to\mathbb R\) is differentiable. Let’s suppose also that \(f\) has a local extreme at the point \(c\in[a,b]\). Then \(c\) must satisfy either \[ c=a, \, c=b, \text{ or } f'(c) = 0. \]
If we’re trying to find where a max/min value occurs, this narrows down the points we have to check infinitely.
Optimization example
Find the the absolute maximum and minimum values of \(f(x) = \frac{3}{4}x^3 - 2x\) restricted to the interval \([0,2]\), as well as where they occur.
Note
The value (max or min) refers to the \(y\)-coordinate.
The location (where it occurs) refers to the \(x\)-coordinate.
Solution
Let’s start with a computer generated graph.
It’s pretty clear that there’s the absolute maximum value of \(y=2\) occurs at \(x=2\). There’s also a local maximum at the origin, though, that’s not the main question.
Solution (cont)
It also looks like the absolute minimum value occurs just to the left of \(x=1\). You can hover over the graph in the interactive version to find that point more precisely to be
- Absolute minimum value is \(y\approx-1.25708\) and
- Absolute minimum occurs at \(x\approx0.94281\).
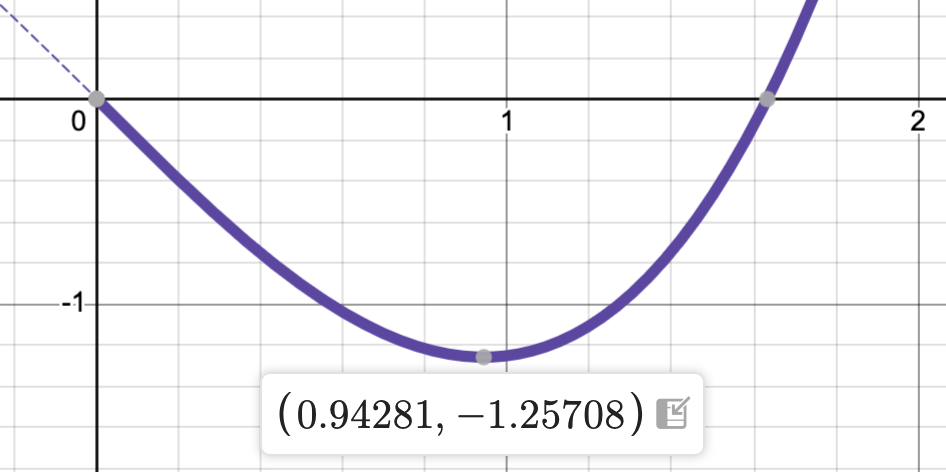
The key question that we can address with the derivative is: what are the exact values?
Solution (finale)
First, we take the derivative and set it equal to zero.
\[f(x) = \frac{3}{4}x^3 - 2x \implies f'(x) = \frac{9}{4}x^2 - 2 \stackrel{\color{red}?}{=}0\]
Solving that last part for \(x\), we find that the absolute minimum occurs at \[x^2 = 8/9 \text{ or } x = \sqrt{8/9}.\]
We can plug back into \(f\) to get the absolute minimum value of \[y = \frac{3}{4}\left(\sqrt{8/9}\right)^3 - 2\sqrt{8/9}.\]
Integration
The integral is also tied to a geometric aspect of the graph of the function - namely signed area. In the graph below, the value of \[ \int_a^b f(x)\,dx \] is exactly the area of the blue region over the \(x\)-axis minus the area of the red region under the \(x\)axis.
Definition
The definite integral is defined in a manner reminiscent of the derivative - i.e. we approximate and then take a limit. For the integral, the approximation takes the form
\[\int_a^b f(x) \, dx \approx \sum_{i=1}^N f(x_i) \, \Delta x,\]
\[\text{where } \Delta x = \frac{b-a}{N} \text{ and } x_i = a+i\Delta x.\]
We then take the limit as \(N\to\infty\) to get the actual value of the integral.
Picture
Just as with the derivative, there’s an image that makes this approximation step more clear:
FTC
Continuing the analogy with differentiation, there’s an algebraic shortcut that makes computing the integral more efficient, at least in some cases. That shortcut is called the Fundamental Theorem of Calculus, or FTC:
Theorem
If \(f:[a,b]\to\mathbb R\) and \(F'(x) = f(x)\) for all \(x\in[a,b]\), then \[\int_a^b f(x) \, dx = F(b)-F(a).\]
Example
\[\begin{aligned} \int_{-1}^1 (1-x^2) \, dx &= 2\int_0^1 (1-x^2) \, dx \\ &= 2\left(x-\frac{1}{3}x^3\right)\bigg\rvert_0^1 \\ &= 2\left(1\frac{1}{3}\right) = 2\times\frac{2}{3} = \frac{4}{3}. \end{aligned}\]
Note that we’ve used the symmetry of the function to simplify the integral in the first step.
\(u\)-substitution
We will not get too heavily into integration in this class. Our most heavy application of integration will be to help us understand probability distributions. In turns out that \(u\)-substitution is particularly useful in that situation.
As an example, suppose we wish to evaluate
\[\int_0^2 x\sqrt{4-x^2} \, dx.\]
Note that the expression \(4-x^2\) is nested inside the square root function and that its derivative (up to a constant multiple) is sitting outside. This suggests that we might try setting \(u=4-x^2\).
Example (cont.)
If \(u=4-x^2\), then \(\frac{du}{dx} = -2x\) so that \(x\,dx = -\frac{1}{2}du\). Thus,
\[\begin{aligned} \int_0^2 x\sqrt{4-x^2} \, dx &= \int_0^2 \sqrt{4-x^2} \, x\, dx = \int_4^0 \sqrt{u} \, \left(-\frac{1}{2}\right)\,du \\ &= \frac{1}{2} \int_0^4 u^{1/2} \, du = \frac{1}{2}\frac{2}{3} u^{3/2}\bigg\rvert_0^4 = \frac{1}{3}4^{3/2} = \frac{8}{3}. \end{aligned}\]
Note that
- We’ve changed the bounds of integration by plugging \(x=0\) and \(x=2\) into \(u=4-x^2\).
- We switched the order of integration after the translation, which simply changes the sign of the integral.
The normal distribution
One of our major uses of integration will be to understand statistical distributions. The first and most widely used such example is the normal distribution.
The normal distribution is defined in terms of two parameters The mean \(\mu\) and the standard deviation \(\sigma\). Given \(\mu\) and \(\sigma\), the probability density function of the corresponding normal distribution has the form
\[f_{\mu,\sigma}(x) = \frac{1}{\sqrt{2\pi}\sigma}e^{-(x-\mu)^2/(2\sigma^2)}.\]
The family album
The normal distribution, is really a whole family of distributions, indexed by \(\mu\) and \(\sigma\). As \(\mu\) and \(\sigma\) change, the picture changes in predictable fashion.
Preservation of area
In addition, these transformations are area preserving.
Area preservation as an integration formula
This area preservation can be explained via the formula
\[ \frac{1}{\sqrt{2\pi}\sigma}\int_a^b e^{-(x-\mu)^2/(2\sigma^2)} \, dx = \frac{1}{\sqrt{2\pi}} \int_{(a-\mu)/\sigma}^{(b-\mu)/\sigma} e^{-x^2/2} \, dx. \]
You might recognize the bounds of integration on the right as the so-called \(z\)-scores of \(a\) and \(b\) from intro statistics. Thus, this formula translates a general normal integral to a standard normal integral obtained when \(\mu=0\) and \(\sigma=1\).
Furthermore, this formula can be derived via \(u\)-substitution.
Proof of the formula
Here’s a justification of the formula. To perform \(u\)-substitution, we let \[u=\frac{x-\mu}{\sigma} \text{ so that } du=\frac{1}{\sigma} dx.\] Then,
\[ \begin{aligned} \frac{1}{\sqrt{2\pi}\sigma} \int_a^b e^{-(x-\mu)^2/(2\sigma^2)} \, dx &= \frac{1}{\sqrt{2\pi}} \int_a^b e^{-\frac{1}{2}\left(\frac{x-\mu}{\sigma}\right)^2} \, \frac{1}{\sigma} dx \\ &= \frac{1}{\sqrt{2\pi}} \int_{(a-\mu)/\sigma}^{(b-\mu)/\sigma} e^{-\frac{1}{2}u^2} \, du \\ &= \frac{1}{\sqrt{2\pi}} \int_{(a-\mu)/\sigma}^{(b-\mu)/\sigma} e^{-x^2/2} \, dx. \end{aligned}\]
Intro stats perspective
Ultimately, the normal distribution is used to compute probabilities that arise in statistics. In that context, typically, \(X\) denotes a normally distributed random variable with mean \(\mu\) and standard deviation \(\sigma\) and \(x\) denotes a value generated by \(X\). We say that the \(Z\)-score of \(x\) is \[ z = \frac{x-\mu}{\sigma}. \] We can then compute probabilities arising from \(X\) using the standard normal \(z\).
Example
Scores on the SAT exam are, by design, normally distributed with mean 500 and standard deviation 100. At what percentile is a score of 700? That is, if we score a 700 on the SAT, then what percentage of folks can we expect scored below our score?
Solution: It’s pretty easy to compute the \(Z\)-score: \[ z = \frac{700-500}{100} = \frac{200}{100} = 2. \] In intro stats, you look up \(2\) in the standard normal table to find \[P(Z<2) \approx 0.9772.\] Thus, we expect our score to be better than nearly \(98\%\) of the folks who took the SAT.
The numerical perspective
Ultimately, the values in a standard normal table are computed via numerical integration. Thus, the statement that \[P(Z<2) \approx 0.9772\] arises from the integral computation \[ \frac{1}{\sqrt{2\pi}}\int_{-\infty}^2 e^{-x^2/2} \, dx \approx 0.9772. \] Which leads us to our final topic in single variable calculus…
Numerical analysis
Our computer lab during the class period will focus on numerical analysis, which I would define as the art and practice of finding numerical estimates to solutions of the classical problems of applied mathematics.
This last topic will give you just a little taste.
A key application
As we just saw, it’s of primary importance to be able to compute integrals of the form
\[ \frac{1}{\sqrt{2\pi}}\int_{a}^b e^{-x^2/2} \, dx. \]
The symbolic attempt
Unfortunately, \(e^{-x^2}\) has no elementary anti-derivative. We can use Python’s symbolic library SymPy to see this.
You can look up erf if you like. The immediate implication of this computation, though, is that there’s no symbolic anti-derivative for the probability density function of the normal distribution. Thus, generally, SymPy can’t compute definite integrals arising from the normal distribution.
Numerical estimates
Python’s fundamental numerical libraries, NumPy and SciPy, can provide precise numerical estimates to these integrals, though.
import numpy as np
from scipy.integrate import quad
quad(lambda x: np.exp(-x**2/2)/np.sqrt(2*np.pi), -2, 1)(0.8185946141203638, 9.088225884305732e-15)Note that the result comes in two parts
- The value of the integral, which is approximately \(0.81859\) and
- An error estimate that implies that the computed result is within \(10^{-14}\) of the actual value.
Optimization
Recall that many machine learning algorithms work by minimizing error produced by a model when applied to tagged training data. Thus, optimization is of fundamental importance for us.
Example
As an example, let’s try to find a minimum value of
\[f(x) = x^2 + 3\sin(5x).\]
A graph
Let’s plot the graph of the function with the minimum that we just found labeled so we can see what’s going on.
Comments
It looks like we found a local minimum, rather than the global minimum. The reason is that the signature of the
minimizefunction iswhere
x0is an initial seed that should be close to the actual root.Moral
It helps to understand the details of an algorithm, even if you’re just using a library that implements it!