Higher period bulbs

Subsection 3.7.5 Higher period bulbs

Figure Figure 3.7.8 shows that there are lots of disk-like bulbs attached to the main cardioid. As \(c\) moves from the main cardioid into one of these bulbs, \(f_c\) bifurcates from having an attractive fixed point, to an orbit of period \(q\) for some integer \(q \gt 1\text{.}\) After the period 2 bulb, the two next largest bulbs near the top and bottom of the main cardioid are period 3 bulbs. The other bulbs have larger period still.

Let's try to gain a quantitative understand of the nature of these bulbs. To do so, we re-consider our description of the main cardioid from subsection Subsection 3.7.2. Again, the interior of the main cardioid can be characterized algebraically as

\begin{align*} f_c(z) &= z\\ |f_c'(z)| &\lt 1. \end{align*}

More generally, though, we can obtain a fixed point with any given multiplier \(\gamma\) that we like by solving

\begin{align*} f_c(z) &= z\\ f_c'(z) &= \gamma. \end{align*}

If we solve this system for \(c\) and \(z\text{,}\) we obtain

\begin{align*} c &= \frac{1}{4} \left(2\gamma - \gamma^2\right)\\ z &= \gamma/2. \end{align*}

Thus, \(f_c\) has a fixed point with multiplier \(\gamma\) at \(\gamma/2\) when \(c=(2\gamma - \gamma^2)/4\text{.}\)

Let us now define \(c(\gamma) = (2\gamma - \gamma^2)/4\) and consider the image of rays of the form \(r\exp(2\pi i \theta)\text{,}\) where \(\theta\) is fixed and \(0\leq r \leq 1\text{.}\) These should all lie within the main cardioid and stretch from zero to a point on the boundary of the cardioid. Some of these are plotted in figure Figure 3.7.9.

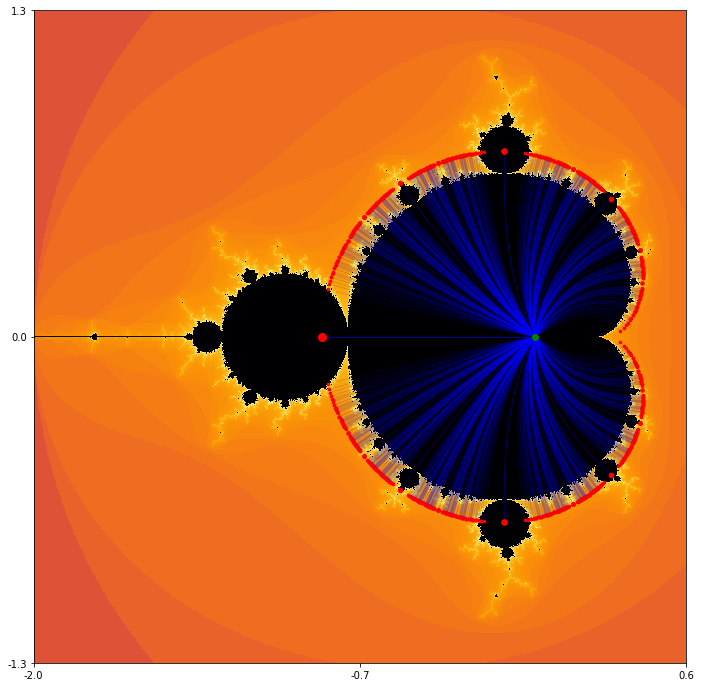
Figure 3.7.9 Bulbs located by the cardioid parametrization

Note that the rays shown in figure Figure 3.7.9 all correspond to rational values of \(\theta\) and, as it appears, a periodic bulb is attached to the main cardioid at every rational ray. Even more is true - if \(\theta=p/q\text{,}\) then the bulb attached to the main cardioid at the point \(c(\exp(2\pi i \theta))\) has period \(q\) and rotation number \(p\text{.}\)

To understand this, recall that \(c(\gamma)\) is built specifically so that \(f_{c(\gamma)}\) will have multiplier \(\gamma\text{.}\) So, what happens to the attractive orbits of \(f_c(\gamma)\) for

\begin{equation*} \gamma = r e^{2\pi i \theta} \end{equation*}

for a fixed rational value of \(\theta\) as \(r\) moves from zero up to one and even just a little bit past? For \(r \lt 1\text{,}\) \(f_c\) has an attractive fixed point. For \(r=1\text{,}\) \(f_c\) has a neutral fixed point with multiplier \(\gamma=\exp(2\pi i \theta)\text{.}\) Note that the geometric effect of multiplying by this particular value of \(\gamma\) is to rotate through the angle \(2\pi\theta=2\pi p/q\text{.}\) If we do this \(q\) times, we've rotated through the angle \(2\pi\theta=2\pi p\text{,}\) which returns to where we started. We might expect an attractive orbit of period \(q\text{;}\) we don't have it yet because the origin still in the basin of the neutral fixed point. Once \(r \gt 1\text{,}\) that fixed point becomes slightly repulsive and the attractive orbit of period \(q\) appears.

Note that each of these bulbs has further bulbs sprouting off and similar considerations apply.