Subsection 3.7.4 The Mandelbrot set as a bifurcation locus
We've now got a solid understanding of the period 1 component of the Mandelbrot set (the main cardioid) and the period 2 component (the period 2 bulb). The period 2 component is called a “bulb” because it is directly attached to the main cardioid. Indeed, using our parametrizations, you can show easily enough that the point \(c=-3/4\) lies on both the boundary of the main cardioid and on the boundary of the period 2 component. Note that, for this value of \(c\text{,}\) \(f_c\) has a neutral fixed point at \(z=-1/2\text{.}\) As \(c\) moves from the main cardioid, through the point \(-3/4\text{,}\) and into the period 2 bulb, the function \(f_c\) undergoes a bifurcation - that is a qualitative change in the global dynamics of the function. More specifically, \(f_c\) changes from having an attractive fixed point to having an attractive orbit of period 2. This is very much like the bifurcation diagram that we saw when studying real iteration. In fact:
The geometric relationship between the Mandelbrot set and the bifurcation diagram is made explicit in figure Figure 3.7.7.
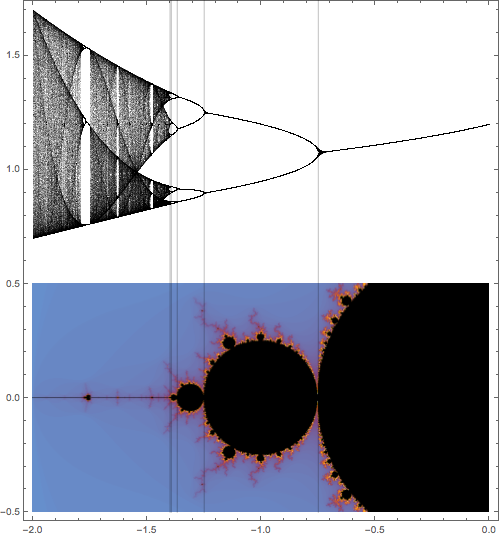
Figure Figure 3.7.7 shows only how the Mandelbrot set aligns with the real bifurcation diagram. There is really much more to the picture, though. All the visible components of the Mandelbrot set correspond to distinct, qualitative behavior. As \(c\) moves within one component, the qualitative behavior of \(f_c\) stays the same. More precisely, any two values of \(c\) chosen from the same component will have attractive orbits of the same period. As \(c\) moves from any component of the Mandelbrot set to another in the complex plane, \(f_c\) undergoes a bifurcation - period doubling, tripling, or whatever. If \(c\) exits the Mandelbrot set, \(f_c\) undergoes a more complicated type of bifurcation.
This all suggests another way to draw the Mandelbrot set. We iterate from the critical point zero, as in algorithm Algorithm 3.6.2, but we stop iteration whenever we find some sort of attractive behavior. We then color the point \(c\) according to the period of the orbit we find and shade it according to how long it took to detect the periodicity. The result is shown in figure Figure 3.7.8.
