Theorem 4.2.1
Let \(f\) be a polynomial.- If all critical orbits of \(f\) are bounded, then the Julia set of \(f\) is connected.
- If all critical orbits of \(f\) diverge to \(\infty\text{,}\) then the Julia set of \(f\) is totally disconnected.
Section 4.2 Critical orbits for polynomials
As we move from quadratic to more general polynomials, a critical difference is the fact that the polynomial may have more than one critical point. This allows for more possibilities in dynamical behavior and geometric properties of the Julia set. The closest analog of Theorem 3.5.1 is the following:
We'll not prove this theorem but we do illustrate it below. We'll also use this theorem to guide us in our exploration of cubic polynomials.
Unlike Theorem 3.5.1, Theorem 4.2.1 is not exhaustive. That is, it's certainly possible for a polynomial to have some bounded critical orbits and some divergent critical orbits. The Julia set of such a polynomial is often composed of infinitely many non-trivial, connected components. Figure 4.2.2 illustrates several possibilities.
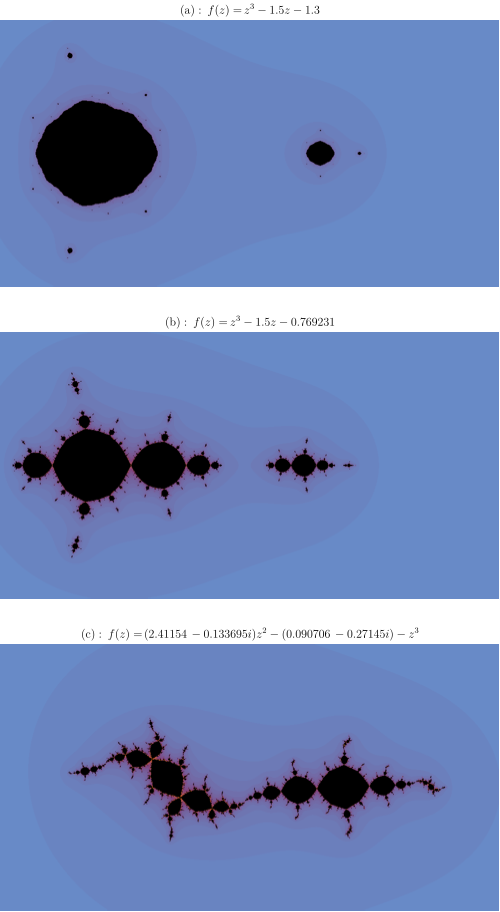
The Julia sets in Figure 4.2.2 were chosen so that
- has one critical orbit attracted to a fixed point and one divergent critical orbit.
- has one critical orbit attracted to an orbit of period two and one divergent critical orbit.
- has one critical orbit attracted to an orbit of period two and one critical orbit attracted to an orbit of period three.