Theorem 5.4.1
Suppose that \(f\) is a rational function with a neutral fixed point at \(z_0\text{.}\) Then \(f\) is linearizable at \(z_0\) if and only if \(z_0\) lies in the Fatou set of \(f\text{.}\)
Section 5.4 Neutral points
The dynamics near a neutral point are considerably more complicated than the other cases. The dynamics depend quite subtely on the number theoretic properties of the mulitplier. For simplicity, we focus on the case where the origin is a neutral fixed point. This is really no restriction. If we have an orbit of degree \(n > 1\text{,}\) rather than a fixed point, then the points of that orbit are neutral fixed points of \(f^n\text{.}\) If the fixed point is not zero, then we can shift that fixed point via conjugation. Thus, we are interested, in this section, in functions of the form
\begin{equation*}
f(z) = \lambda z + O(z^2),
\end{equation*}
where \(|\lambda=1|\text{.}\)
There are a number of theorems that outline the possibilities that we will not prove, though we will use them to guide our exploration.
Theorem 5.4.2
Suppose that \(f\) is a rational function with a neutral fixed point at \(z_0\) that lies in some component of the Fatou set of \(f\text{.}\) Then, that component is simply connected and \(f\) is conjugate to a rotation of infinite order about \(z_0\)
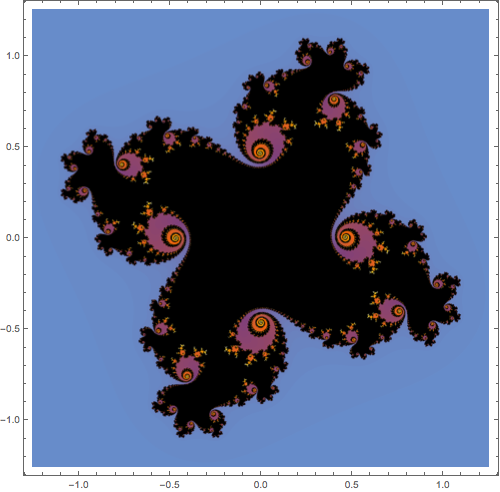
Theorem Theorem 5.4.2 implies immediately that for for a neutral point \(z_0\) with multiplier \(\lambda = e^{2\pi\alpha i}\) to lie in the Fatou set, the number \(\alpha\) must be irrational. It can be proved that most irrational \(\alpha\) (in the measure theoretic sense) work. One example is shown in figure Figure 5.4.3. It would be instructive to play with that Julia set in a dynamic setting.
It can also be proved that there are irrational numbers \(\alpha\) and functions \(f\) with a fixed point \(z_0\) with multiplier \(\lambda=e^{2\pi\alpha i}\) such that \(z_0\) lies in the Julia set of \(f\text{.}\) Such Julia sets are not well understood and at least some of them are known to be uncomputable in polynomial time. To the best of my knowledge, no useful images of such Julia sets have ever been produced.