Figure Figure 3 illustrates a linearizing conjugacy for \(f(z)=z^2-z/2\text{.}\) The red point is the origin. The curves emanating out of that point map to rays of constant argument under \(\varphi\text{;}\) the loops around that point (only one is explicit) map to circles of constant absolute value. There are many other points that have the same general appearance as the origin; those are pre-images of the origin under \(f\) or \(f^n\) for some \(n\text{.}\) Put another way, those points eventually map onto the origin under iteration of \(f\text{.}\) As we move away from the origin, the curves congregate on the Julia set of \(f\text{.}\) Outside of the Julia set appears blank as that's outside the domain of \(\varphi\text{.}\)

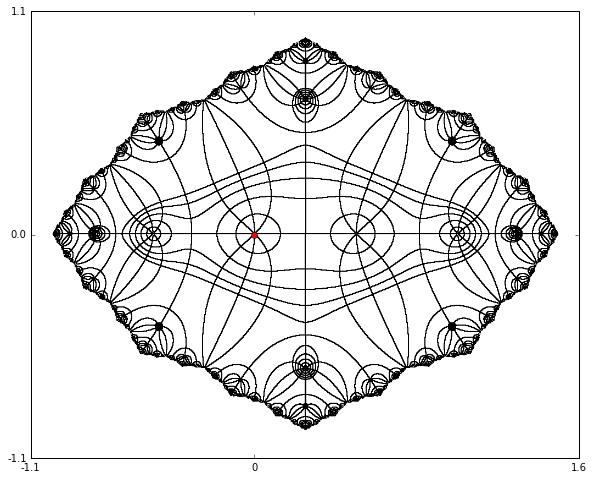
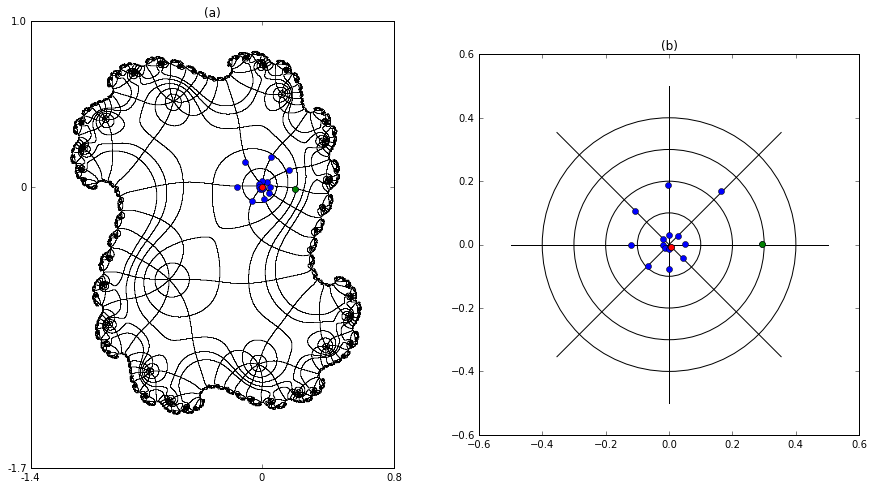
Figure Figure 4 (a) illustrates a linearizing conjugacy for \(f(z)=z^2+0.8e^{\pi i/4}z\text{.}\) In addition, the figure shows an orbit that spirals into an attractive fixed point. Since \(f'(0)=0.8e^{\pi i/4}\text{,}\) the angle rotation from one point to the next is close to \(\pi/4\text{,}\) though the first few deviate measurably from that due to the \(z^2\) term. Figure Figure 4 (b) plots the image of those points under \(\varphi\) on a polar grid. As expected, they follow an orbit under iteration of the linear function \(L(z)= 0.8e^{\pi i/4}z\text{.}\)