Showing perpendicularity at every point?

asked 2014-07-02 14:33:18 -0600

Justin
1009 ●2 ●20 ●38

updated 2014-07-02 15:37:55 -0600

This is from a few days ago, but I am curious how one would prove this. Exercise 13.2.8 reads:

Suppose that $\left|\textbf{r}(t) \right| = k$, for some constant $k$. This means that $ \textbf{r} $ describes some path on the sphere of radius $k$ with center at the origin. Show that $ \textbf{r} $ is perpendicular to $\textbf{r}'$ at every point. Hint: Use Theorem 13.2.5, part (d).

Theorem 13.2.5 part (d) states:

$$\frac{d}{dt} (\textbf{r}(t) \cdot \textbf{s}(t)) = \textbf{r}'(t) \cdot \textbf{s}(t) + \textbf{r}(t) \cdot \textbf{s}'(t) $$

I'm just not sure where to begin. If someone could give me a starting point, I would really appreciate it!

edit retag flag offensive close delete

2

answered 2014-07-08 05:49:53 -0600

Mark
166 ●1 ●5 ●12 https://sites.google.com/...

updated 2014-07-08 06:26:06 -0600

This is a hard one, so here's my answer. Suppose that $\textbf{r}(t)$ is a vector valued function of constant magnitude. I'm going to compute

$$\frac{d}{dt} (\textbf{r}(t) \cdot \textbf{r}(t))$$

in two ways. First, the dot product rule states that

$$ \frac{d}{dt} (\textbf{r}(t) \cdot \textbf{r}(t)) = \textbf{r}'(t) \cdot \textbf{r}(t) + \textbf{r}(t) \cdot \textbf{r}'(t) = 2 \; \textbf{r}(t) \cdot \textbf{r}'(t). $$

On the other hand, since $\textbf{r}(t)$ has constant magnitude, we know that $\textbf{r}(t) \cdot \textbf{r}(t) = \||\textbf{r}(t)\||^2$ is constant. Thus,

$$\frac{d}{dt} (\textbf{r}(t) \cdot \textbf{r}(t)) = 0.$$

As result, these two computations must be equal so we have

$$2 \; \textbf{r}(t) \cdot \textbf{r}'(t) = 0,$$

which only happens if

$$\textbf{r}(t) \cdot \textbf{r}'(t) = 0.$$

Examples

The standard example $\textbf{r}(t) = \langle \cos(t), \sin(t) \rangle$, which satisfies $\||\textbf{r}(t)\||=1$. Since, $\textbf{r}'(t) = \langle -\sin(t), \cos(t) \rangle$, it's easy to see that $\textbf{r}(t) \cdot \textbf{r}'(t)=0$. Geometrically, this states that the velocity vector of uniform circular motion is perpendicular to the position vector, which only makes all the sense in the world.

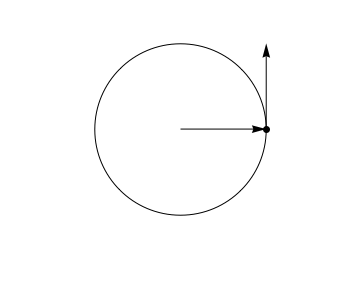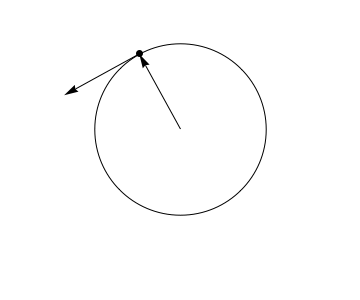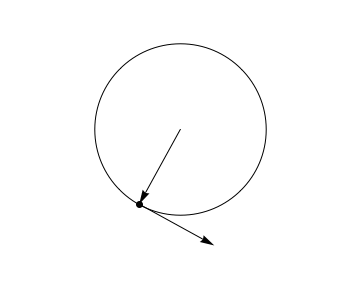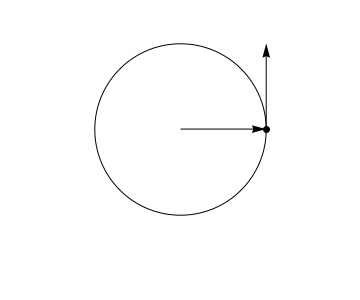
image description

It's important to realize, though, that the theorem is much more general than that. The motion need not be uniform at all.

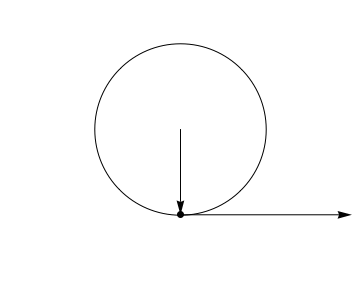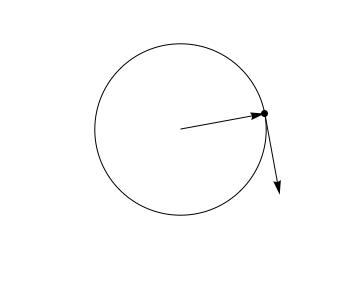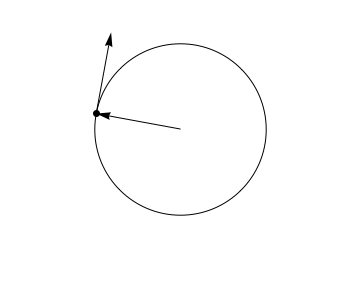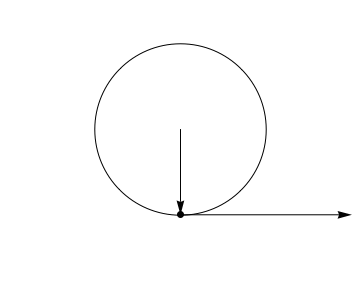
image description

The motion could even be in 3D along a sphere.

edit flag offensive delete publish link

2

answered 2014-07-02 18:26:11 -0600

Christina
807 ●18 ●35 https://sites.google.com/...

updated 2014-07-03 06:13:57 -0600

Taking a stab at this one...

What if we use Th. 13.2.5 part d as follows by using vector functions and allowing k to be the radius since that is what the problem tells us.

Does the following show what we want, or am I missing any elements? This is also allowing one of the planes to be zero.

$$\frac{d}{dt} r(t) \cdot r(t) = \langle k\cos(t), k\sin(t)\rangle \cdot \langle k\cos(t) , k\sin(t)\rangle$$ $$= \langle k\cos(t), k\sin(t)\rangle \cdot \langle -k\sin(t), k\cos(t) \rangle + \langle k\cos(t) , k\sin(t) \rangle \cdot \langle -k\sin(t) , k\cos(t) \rangle$$ $$= -k^2 \cos(t) \sin(t) + k^2 \sin(t) \cos(t) - k^2 \cos(t) \sin(t) + k^2 \sin(t) \cos(t)$$

Here we can see the answer is zero! What do you think?

Clarification Added What I wanted to say was that even though the answer is zero, it also shows that the dot product of $\vec{r}$ and $ \vec{r '}$ is zero...$$= \large[\small-k^2 \cos(t) \sin(t) + k^2 \sin(t) \cos(t)\large]\small + \large[\small - k^2 \cos(t) \sin(t) + k^2 \sin(t) \cos(t)\large]$$

edit flag offensive delete publish link

Showing perpendicularity at every point?

2 Answers

Question tools

Stats

Related questions