asked 2014-06-30 09:26:18 -0600
I'm pretty confident that I understand how to parametrize the bug's movement. But I don't understand what kind of movement I need to parametrize. can someone clarify the bugs movement in non-mathematical terms. Is the wheel moving in any dimension or just spinning?
answered 2014-06-30 12:54:39 -0600
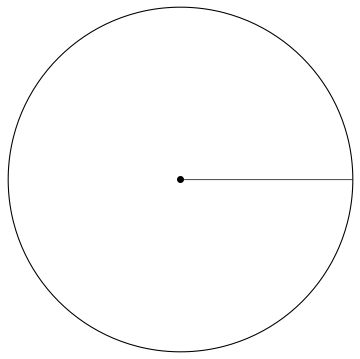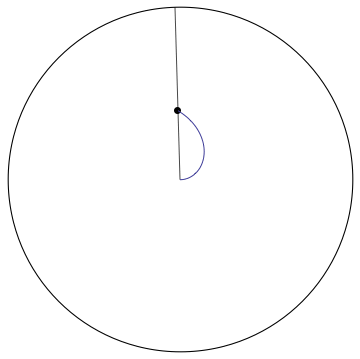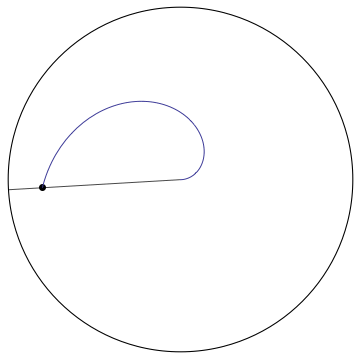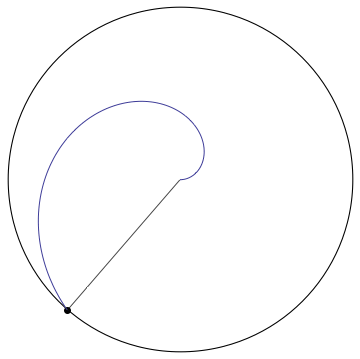
The problem says the the wheel is rotating at $12 \frac{rad}{s}$, with the center at the origin. Since the problem says the wheel is "rotating", and not "rolling", we know that the wheel is just spinning. Since the wheel is rotating and the bug is on it, (assuming he is no longer at the dead center) we know that the bug is going around the origin in circular motion of radius $R$. The bug is crawling along one of the spokes at a constant speed of $3 \frac{units}{s}$, so we also know that the radius of the circle that the bug is traveling on is changing at $3 \frac{units}{s}$. Therefore we know that as the bug traces out the circle the radius gets bigger tracing out a spiral.
I know that you only asked for the conceptual, but for any one else who will have a question on the math, ill explain that too.
To represent this mathematically we will break it into linear motion and circular motion. I will represent the linear motion of the bug by the distance away from origin, and the circular motion by the position of the spoke he is crawling on. We know that the bug is crawling away from the center of the origin at a constant rate of of $3 \frac{units}{s}$, since the center of rotation is at the origin, and the bug is always crawling away from the origin the radius is simply represented by $3\frac{units}{s}$ multiplied by time $t$ or. $$R = 3\frac{units}{s} * t$$ $$ R= 3t$$ The circular motion of the bug is represented by a simple circle, we know that a unit circle on the xy plane can be represented by $$\overrightarrow P(t)=\langle cos(t),sin(t),0\rangle$$ but since our wheel is rotating in the yz plane (the problem said xz plane, but this was a typo) we must make the circle in the yz plane by changing our equation to $$\overrightarrow P(t)=\langle 0,cos(t),sin(y)\rangle$$ We know that the bug initially crawls up the +y axis so the initial direction (at $t=0$) must be in the +y direction. If we set the $y$ component equal to $sin(t)$ and $z$ componet equal to $cos(t)$ we get $$\overrightarrow P(t)=\langle 0,sin(t),cos(t)\rangle$$ at $t=0$, $ y=sin(0)=0$ and the $z=cos(0)=1$ therefore in order to make +y the starting direction we make $y=cos(t)$ and $z=sin(t)$ giving us the equation $$\overrightarrow P(t)=\langle 0,cos(t),sin(y)\rangle$$ The problem states that the wheel is rotating at $12 \frac{rad} {s}$, since the unit circle rotates at $1 \frac{rad} {s}$, we must multiply the $t$'s in the equation by 12 so the circle will rotate 12 times faster. This gives us $$\overrightarrow P(t)= \langle 0,cos(12t), sin(12t)\rangle$$ $Note$ I have noticed that people have been wanting to convert to $\frac{radians}{second}$, but remember that the only things you can plug into sine and cosine are $degrees$ and $radians$.
Now we must combine the linear and circular motion, to do this we multiply the unit circle equation by the radius to obtain the position equation. Since our circle is represented by a vector in a parametric equation and the radius is a multiplier, we can use scalar multiplication and distribute the radius over the vector $$\overrightarrow P(t)=\langle 0,Rcos(12t),Rsin(12t)\rangle $$
Finally we plug in the R value of $R=3t$ and we get our anwser
$$\overrightarrow P(t)=\langle 0,3tcos(12t),3tsin(12t)\rangle$$
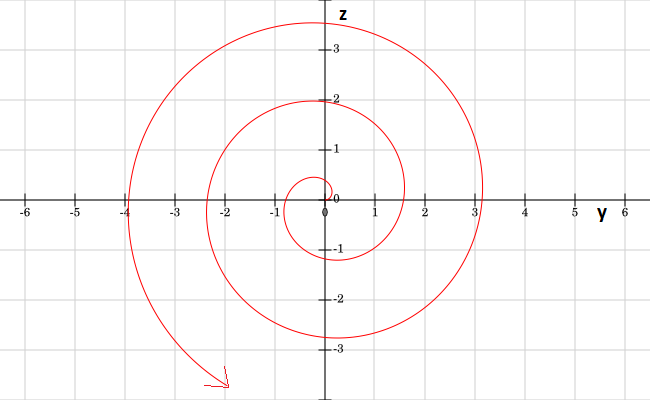
or a modified 3d graph of jlubin's to support my theory.
Comment: Very nice! I think I like the $12t$ here better than the $6/\pi$ in the other answer.
answered 2014-06-30 12:40:31 -0600
I am in agreement with Tiffany up to a point. I am picturing the wheel spinning at 12 radians per second around the xz plane but not moving in any y direction.
As the bug walks along the spoke at 3 units per second, however, you also have the circular motion. Wouldn't this make the linear motion 3(t) times the circular motion? Because as the wheel spins, the bug will in fact be moving in both the x and the z directions.
Using 12 radians per second and a value of zero for the y axis would give us $$\vec p(t) = \langle(3t)\cos(12t),0, (3t)\sin(12t)\rangle$$
Like Tiffany, I would also like more input, comments, etc. And we need to generate at least 2 more questions!!!! Tiffany, maybe we should have made our answers in the form of questions, or would that be cheating? JK
Comment: Very good, though I'm not sure about the $6/\pi$.
Edit made I have edited my previous version to reflect the correct use of 12 radians per second...
answered 2014-06-30 11:49:00 -0600
In class he said to picture the wheel being stationary. So from my understanding with the wheel being in the xz plane it is rotating with it's center being (0,0,0). Picture a bicycle lifted for maintenance, the front tire spins freely without actually rolling anywhere. The bug is crawling outwards(from (0,0,0) towards edge of rim) on the spoke, while the spoke is spinning with the wheel at 12 radians per second. So from what I understand, we have to take the bugs motion, which is linear, and factor in the fact that the spoke he is crawling on is also moving, but in a circular motion. So the bugs movement should be something like p(t) =$\langle0,0,3\rangle t$ (supposing the spoke lies along the positive z axis) and the circular motion being p(t) =$ \langle \cos(t),0,\sin(t)\rangle $,(since the wheel is a circle) now since the wheel is spinning at 12 radians per second, this is about 1.9 revolutions per second $ \frac {12radians}{second}$ * $ \frac{1revolution}{2\pi radians}$=1.9$\frac{revolution}{second}$ . So this now makes your circular motion p(t) = $\langle \cos(1.9t),0,\sin(1.9t)\rangle$ . Now as far as him saying we have to do some multiplication to get the final vector function I'm not sure. I don't know if this will help you at all, but hopefully someone else can help elaborate further from this point, or clarify further for the two of us.
added on later I'm not sure if this is even close to being right, but when I thought more about him saying we needed to multiply the two, I ended up coming up with p(t)= $\langle3t(cos(1.9t)),0,3t(sin(1.9t))\rangle$
Since the bugs motion is 3 units per second, it would make sense that for every t he would move 3 units, so multiplying that into the circular motion of the wheel is how I ended up with the above equation.
*Since comments aren't being allowed to be added, Christina we should have done our answers as questions! :) and after I thought more on mine, I ended up having the same answer as you, I just used 1.9 instead of $\frac{6}{\pi}$ I also didn't include the y axis in any of my answers, so I went back and just added those in. So at least we both ended up with the same answer! **
answered 2014-06-30 13:17:59 -0600
I have changed the equation slightly to reflect cbass's answer. The coefficient inside the sinusoidal functions has changed from $\frac{6}{\pi}$ to $12$. This is an animated graph updated to reflect it.
I made an interactive Desmos graph to help anyone visualize the answers of Christina and Tiffany. Here is the link. (The blue point represents the bug, and the black lines are the wheel and the spokes.)
Just to clarify, I believe that when we have to multiply the position functions together, we must do something like this:
Let $ l(t) $ be the linear motion, $ \vec c(t) $ be the circular motion, and $ \vec p (t) $ be the overall position.
$$ l(t) = 3t$$ $$ \vec c(t) = \langle \cos \left( \frac{6}{\pi} t \right), \sin \left( \frac{6}{\pi} t \right) \rangle $$ $$ \vec p(t) = l(t) * \vec c(t) = (3t) \langle \cos \left( \frac{6}{\pi} t \right), \sin \left( \frac{6}{\pi} t \right) \rangle = \langle 3t * \cos \left(\frac{6}{\pi} t \right), 3t * \sin \left( \frac{6}{\pi} t \right) \rangle $$
The $ l(t) * \vec c(t) $ is scalar multiplication.
Comment: Very nice! Is it possible to include the path of the bug in your animation? Something like so:
Asked: 2014-06-30 09:26:18 -0600
Seen: 114 times
Last updated: Jul 01 '14
Copyright Askbot, 2010-2011. Content on this site is licensed under a Creative Commons Attribution Share Alike 3.0 license.
