Revision history [back]
I made an interactive Desmos graph to help anyone visualize the answers of Christina and Tiffany. Here is the link. (The blue point represents the bug, and the black lines are the wheel and the spokes.)
Just to clarify, I believe that when we have to multiply the position functions together, we must do something like this:
Let $ l(t) $ be the linear motion, $ \vec c(t) $ be the circular motion, and $ \vec p (t) $ be the overall position.
$$ l(t) = 3t$$ $$ \vec c(t) = \langle \cos \left( \frac{6}{\pi} t \right), \sin \left( \frac{6}{\pi} t \right) \rangle $$ $$ \vec p(t) = l(t) * \vec c(t) = (3t) \langle \cos \left( \frac{6}{\pi} t \right), \sin \left( \frac{6}{\pi} t \right) \rangle = \langle 3t * \cos \left(\frac{6}{\pi} t \right), 3t * \sin \left( \frac{6}{\pi} t \right) \rangle $$
The $ l(t) * \vec c(t) $ is scalar multiplication.
 | 2 | No.2 Revision |
I made an interactive Desmos graph to help anyone visualize the answers of Christina and Tiffany. Here is the link. (The blue point represents the bug, and the black lines are the wheel and the spokes.)
Just to clarify, I believe that when we have to multiply the position functions together, we must do something like this:
Let $ l(t) $ be the linear motion, $ \vec c(t) $ be the circular motion, and $ \vec p (t) $ be the overall position.
$$ l(t) = 3t$$ $$ \vec c(t) = \langle \cos \left( \frac{6}{\pi} t \right), \sin \left( \frac{6}{\pi} t \right) \rangle $$ $$ \vec p(t) = l(t) * \vec c(t) = (3t) \langle \cos \left( \frac{6}{\pi} t \right), \sin \left( \frac{6}{\pi} t \right) \rangle = \langle 3t * \cos \left(\frac{6}{\pi} t \right), 3t * \sin \left( \frac{6}{\pi} t \right) \rangle $$
The $ l(t) * \vec c(t) $ is scalar multiplication.
Comment: Very nice! Is it possible to include the path of the bug in your animation? Something like so:
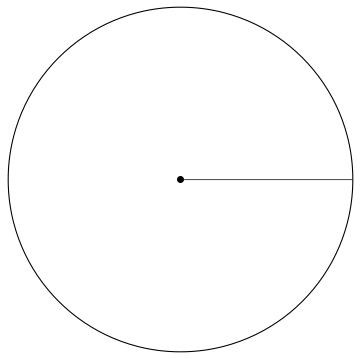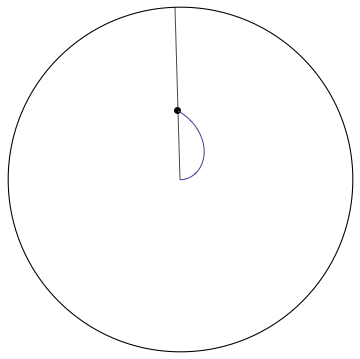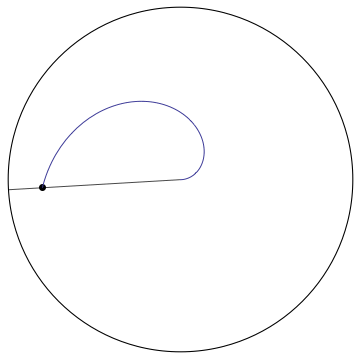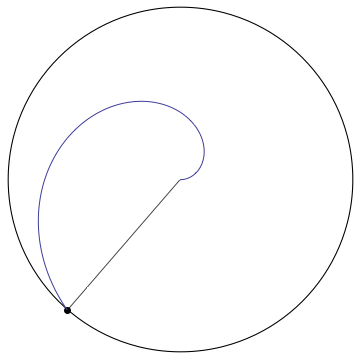
 | 3 | No.3 Revision |
Updated Answer
I have changed the equation slightly to reflect cbass's answer. The coefficient inside the sinusoidal functions has changed from $\frac{6}{pi}$ to $12$. This is an animated graph updated to reflect it.
Original Answer
I made an interactive Desmos graph to help anyone visualize the answers of Christina and Tiffany. Here is the link. (The blue point represents the bug, and the black lines are the wheel and the spokes.)
Just to clarify, I believe that when we have to multiply the position functions together, we must do something like this:
Let $ l(t) $ be the linear motion, $ \vec c(t) $ be the circular motion, and $ \vec p (t) $ be the overall position.
$$ l(t) = 3t$$ $$ \vec c(t) = \langle \cos \left( \frac{6}{\pi} t \right), \sin \left( \frac{6}{\pi} t \right) \rangle $$ $$ \vec p(t) = l(t) * \vec c(t) = (3t) \langle \cos \left( \frac{6}{\pi} t \right), \sin \left( \frac{6}{\pi} t \right) \rangle = \langle 3t * \cos \left(\frac{6}{\pi} t \right), 3t * \sin \left( \frac{6}{\pi} t \right) \rangle $$
The $ l(t) * \vec c(t) $ is scalar multiplication.
Comment: Very nice! Is it possible to include the path of the bug in your animation? Something like so:

 | 4 | No.4 Revision |
Updated Answer
I have changed the equation slightly to reflect cbass's answer. The coefficient inside the sinusoidal functions has changed from $\frac{6}{pi}$ $\frac{6}{\pi}$ to $12$. This is an animated graph updated to reflect it.
Original Answer
I made an interactive Desmos graph to help anyone visualize the answers of Christina and Tiffany. Here is the link. (The blue point represents the bug, and the black lines are the wheel and the spokes.)
Just to clarify, I believe that when we have to multiply the position functions together, we must do something like this:
Let $ l(t) $ be the linear motion, $ \vec c(t) $ be the circular motion, and $ \vec p (t) $ be the overall position.
$$ l(t) = 3t$$ $$ \vec c(t) = \langle \cos \left( \frac{6}{\pi} t \right), \sin \left( \frac{6}{\pi} t \right) \rangle $$ $$ \vec p(t) = l(t) * \vec c(t) = (3t) \langle \cos \left( \frac{6}{\pi} t \right), \sin \left( \frac{6}{\pi} t \right) \rangle = \langle 3t * \cos \left(\frac{6}{\pi} t \right), 3t * \sin \left( \frac{6}{\pi} t \right) \rangle $$
The $ l(t) * \vec c(t) $ is scalar multiplication.
Comment: Very nice! Is it possible to include the path of the bug in your animation? Something like so:

 | 5 | No.5 Revision |
Updated Answer
I have changed the equation slightly to reflect cbass's answer. The coefficient inside the sinusoidal functions has changed from $\frac{6}{\pi}$ to $12$. This is an animated graph updated to reflect it.
Original Answer
I made an interactive Desmos graph to help anyone visualize the answers of Christina and Tiffany. Here is the link. (The blue point represents the bug, and the black lines are the wheel and the spokes.)
Just to clarify, I believe that when we have to multiply the position functions together, we must do something like this:
Let $ l(t) $ be the linear motion, $ \vec c(t) $ be the circular motion, and $ \vec p (t) $ be the overall position.
$$ l(t) = 3t$$ $$ \vec c(t) = \langle \cos \left( \frac{6}{\pi} t \right), \sin \left( \frac{6}{\pi} t \right) \rangle $$ $$ \vec p(t) = l(t) * \vec c(t) = (3t) \langle \cos \left( \frac{6}{\pi} t \right), \sin \left( \frac{6}{\pi} t \right) \rangle = \langle 3t * \cos \left(\frac{6}{\pi} t \right), 3t * \sin \left( \frac{6}{\pi} t \right) \rangle $$
The $ l(t) * \vec c(t) $ is scalar multiplication.
Comment: Very nice! Is it possible to include the path of the bug in your animation? Something like so:

