Number 6 on Exam 2

answered 2014-07-28 16:41:58 -0600

Christina
807 ●18 ●35 https://sites.google.com/...

updated 2014-07-30 18:20:31 -0600

I actually missed this one on the exam, but since then have worked on what the contour diagram would look like. This should help along with what Professor McClure said in class.

(I am very much a beginner with Mathematica) But, if you can find your points on the circle, $(\frac{1}{2}, {\frac{\sqrt{3}}{2}})$ and $(\frac{1}{2}, -{\frac{\sqrt{3}}{2}})$, those points are where a contour would be tangent to the circle. Those are both maxima because as your contours move to the right, your function is set to a larger and larger constant. Likewise, looking on the left you can see a point of tangency where y=0. That is a minima, (-1,0).

This is a basic explanation and hopefully someone else will have more to add.

COMMENT ADDED After playing around with Mathematica I have generated another image that may help with the confusion. If you look at the previous image, the point of tangency at (1,0) is not a maximum. If you look at the new one below, you can see two points of tangency on the top and bottom of the circle (well, they are close, but I am sure you can see what I mean:) These are the maxima, $(\frac{1}{2},\frac{\sqrt{3}}{2})$ and $(\frac{1}{2},-\frac{\sqrt{3}}{2})$. Professor McClure talked about "walking around the outside of the circle and coming upon the points of tangency". I am trying to think of it as the contours having to be outside of the restricted area up until the point of tangency, not inside like the first image.

These points come from the following calculations: $$\nabla f=<1,2y>$$

$$\nabla g=<2x,2y>$$ $$1=2\lambda x $$ solving for $$x=\frac{1}{\lambda2}$$

Now the y components $$2y=2\lambda y$$

$$ 2y-\lambda2y=0$$ $$2y(1-\lambda)=0$$ this gives us $$y=0$$ and $$\lambda = 1$$ Since$$x^2+y^2=1$$

Then for $y=0$ we know $x=-1$ based on our drawing. This gives us the minima at (-1,0). Now to consider

$$x=1/2\lambda$$ Since $\lambda = 1, x=\frac{1}{2}$ Making $$y=\pm \sqrt {3/4}$$ Giving us the points: $$(1/2,\frac{\sqrt {3}}{2})$$ $$(1/2,-\frac{\sqrt {3}}{2})$$.

answered 2014-07-30 18:17:45 -0600

Justin
1009 ●2 ●20 ●38

updated 2014-07-30 18:36:54 -0600

I'll take a stab at answering this, although I admit that I missed this on the exam as well! Here is what the question boils down to:

Use the method of Lagrange multipliers to find the extremes of $f(x, y) = x + y^2$ subject to the constraint $x^2 + y^2 = 1$.

To solve this problem, I will let $g(x, y) = x^2 + y^2$. Therefore:

$$\nabla f = \langle 1, 2y \rangle $$ $$\nabla g = \langle 2x, 2y \rangle $$

I will now set $\nabla f = \lambda \nabla g$. Two vectors are equal if and only if their components are equal. I will also add in the constraint curve to this system of equations so we will have a system of three equations in three variables (i.e. we can solve it).

$$ 1 = 2\lambda x $$ $$ 2y = 2\lambda y $$ $$ x^2 + y^2 = 1$$

Solving for $x$ in our first equation yields $x = \frac{1}{2\lambda}$. The second equation is a bit tricky to solve for $y$. You have to think about it for a second, since you cannot just divide by $y$ on both sides (or something similar). In this equation, $y$ must equal $0$ or $\lambda$ must equal $1$. I will examine both of these possibilities, but for now let us just consider the case where $y = 0$. Here is what our third equation looks like in this case:

$$\left(\frac{1}{2\lambda}\right)^2 + 0^2 = 1$$ $$\frac{1}{4\lambda^2} = 1$$ $$4\lambda^2 = 1$$ $$\lambda^2 = \frac{1}{4}$$ $$\lambda = \pm \frac{1}{2}$$

In the case of a negative lambda:

$$x = \frac{1}{2 * \left(-\frac{1}{2}\right)} = -1 $$ $$ y = 0 $$

Note that $y$ is independent of $x$ and $\lambda$ and is always equal to zero in this case.

In the case of a positive lambda:

$$x = \frac{1}{2 * \left(\frac{1}{2}\right)} = 1 $$ $$ y = 0 $$

This means that our extremes so far are $(-1, 0)$ and $(1, 0)$. However, we have not considered the case where $\lambda = 1$. If $\lambda = 1$, then:

$$x = \frac{1}{2 * 1} = \frac{1}{2}.$$

Here is what our third equation looks like in the case of $\lambda = 1$:

$$ \left(\frac{1}{2}\right)^2 + y^2 = 1$$

Solving for $y$ yields:

$$ \frac{1}{4} + y^2 = 1$$ $$ y^2 = 1 - \frac{1}{4} $$ $$ y^2 = \frac{3}{4} $$ $$ y = \pm \frac{\sqrt{3}}{2} $$

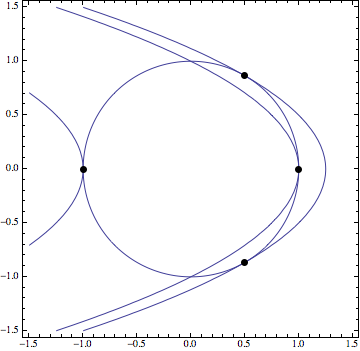
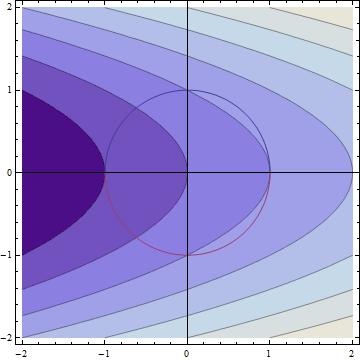
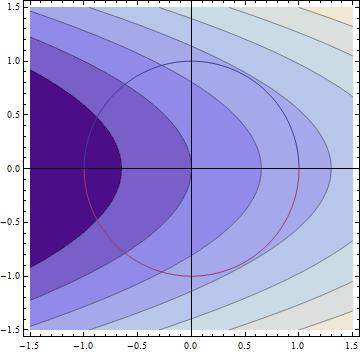
Therefore our four extremes are $(-1, 0)$, $(1, 0)$, $(\frac{1}{2}, -\frac{\sqrt{3}}{2})$, and $(\frac{1}{2}, \frac{\sqrt{3}}{2})$. If we take a look at our contour plot, we can see that the maximums occur at $(\frac{1}{2}, -\frac{\sqrt{3}}{2})$ and $(\frac{1}{2}, \frac{\sqrt{3}}{2})$.

Here are our four points and relevant contours:

answered 2014-07-30 17:02:43 -0600

Tiffany
656 ●3 ●18 ●34

I missed parts of this questions as well (one being my drawing being backwards :( ). But I found my max and min to be : max - (1.0) and min - (-1,0).

I started the same way as you with the $ x= \frac 1{2\lambda}$ and $ 2y = \lambda 2y$ which I solved out to get $ y = \lambda y$. also with my third equation being $ x^2 + y ^2 = 1$

from here I solved my y equation to find that y = 0. Which looking back now, I'm not sure exactly how I came up with that, so maybe thats where I went wrong as well. But I'll continue..

Using y = 0 I then plugged into our 3rd equation to get $$ \frac 1{2\lambda} ^2 + 0^2 = 1$$ $$ \frac 1{4\lambda ^2} = 1$$ $$ 1 = 4\lambda ^2 $$ $$ \frac 14 = \lambda ^2$$ $$ \sqrt \frac 14 = \lambda$$ $$ \lambda = ^+ _- \frac 12$$

From here I went back and plugged $^+_- \frac 12$ back into our first two equations to find that... $$\frac 1{2(\frac 12)} = x = 1$$ and $$ \frac 1{2(-\frac 12)} = x = -1$$ $$ y = 0$$

I hope that this will help at least a little bit, or if someone could clarify where I went wrong as well.