Revision history [back]
I actually missed this one on the exam, but since then have worked on what the contour diagram would look like. This should help along with what Professor McClure said in class.
(I am very much a beginner with Mathematica) But, if you can find your points on the circle, $(\frac{1}{2}, \sqrt{\frac{3}{4}})$ and $(\frac{1}{2}, -\sqrt{\frac{3}{4}})$, those points are where a contour would be tangent to the circle. Those are both maxima because as your contours move to the right, your function is set to a larger and larger constant. Likewise, looking on the left you can see a point of tangency where y=0. That is a minima, (-1,0).
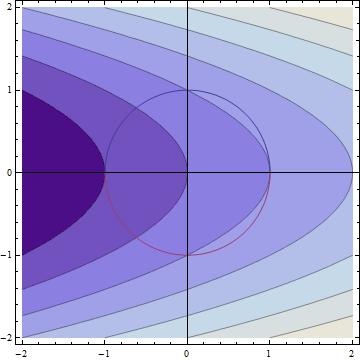
This is a basic explanation and hopefully someone else will have more to add.
 | 2 | No.2 Revision |
I actually missed this one on the exam, but since then have worked on what the contour diagram would look like. This should help along with what Professor McClure said in class.
(I am very much a beginner with Mathematica) But, if you can find your points on the circle, $(\frac{1}{2}, \sqrt{\frac{3}{4}})$ {\frac{\sqrt{3}}{2}})$ and $(\frac{1}{2}, -\sqrt{\frac{3}{4}})$, -{\frac{\sqrt{3}}{2}})$, those points are where a contour would be tangent to the circle. Those are both maxima because as your contours move to the right, your function is set to a larger and larger constant. Likewise, looking on the left you can see a point of tangency where y=0. That is a minima, (-1,0).

This is a basic explanation and hopefully someone else will have more to add.
 | 3 | No.3 Revision |
I actually missed this one on the exam, but since then have worked on what the contour diagram would look like. This should help along with what Professor McClure said in class.
(I am very much a beginner with Mathematica) But, if you can find your points on the circle, $(\frac{1}{2}, {\frac{\sqrt{3}}{2}})$ and $(\frac{1}{2}, -{\frac{\sqrt{3}}{2}})$, those points are where a contour would be tangent to the circle. Those are both maxima because as your contours move to the right, your function is set to a larger and larger constant. Likewise, looking on the left you can see a point of tangency where y=0. That is a minima, (-1,0).

This is a basic explanation and hopefully someone else will have more to add.
COMMENT ADDED After playing around with Mathematica I have generated another image that may help with the confusion. If you look at the previous image, the point of tangency at (1,0) is not a maximum. If you look at the new one below, you can see two points of tangency on the top and bottom of the circle (well, they are close, but I am sure you can see what I mean:) These are the maxima, $(\frac{1}{2},\frac{\sqrt{3}}{2})$ and $(\frac{1}{2},-\frac{\sqrt{3}}{2})$. Professor McClure talked about "walking around the outside of the circle and coming upon the points of tangency". I am trying to think of it as the contours having to be outside of the restricted area up until the point of tangency, not inside like the first image.
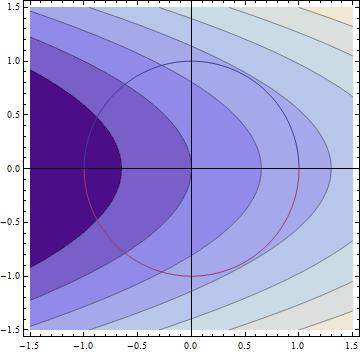
These points come from the following calculations: $$\nabla f=<1,2y>$$
$$\nabla g=<2x,2y>$$
$$1=2\lambda x - solving for x=\frac{\lambda}{2}$$ $$2y=2\lambda y$$ here setting equal to zero $$ 2y-\lambda2y=0$$ $$2y(1-\lambda)=0$$ this gives us $$y=0$$ and $$\lambda = 1$$ Since$$x^2+y^2=1$$
Then for $y=0$ we know $x=-1$ based on our drawing. This gives us the minima at (-1,0). Now to consider
$$x=1/2\lambda$$ Since $\lambda = 1, x=\frac{1}{2}$ Making $$y=\pm \sqrt {3/4}$$ Giving us the points: $$(1/2,\sqrt {3/4)}$$ $$(1/2,-\sqrt {3/4)}$$.
 | 4 | No.4 Revision |
I actually missed this one on the exam, but since then have worked on what the contour diagram would look like. This should help along with what Professor McClure said in class.
(I am very much a beginner with Mathematica) But, if you can find your points on the circle, $(\frac{1}{2}, {\frac{\sqrt{3}}{2}})$ and $(\frac{1}{2}, -{\frac{\sqrt{3}}{2}})$, those points are where a contour would be tangent to the circle. Those are both maxima because as your contours move to the right, your function is set to a larger and larger constant. Likewise, looking on the left you can see a point of tangency where y=0. That is a minima, (-1,0).

This is a basic explanation and hopefully someone else will have more to add.
COMMENT ADDED After playing around with Mathematica I have generated another image that may help with the confusion. If you look at the previous image, the point of tangency at (1,0) is not a maximum. If you look at the new one below, you can see two points of tangency on the top and bottom of the circle (well, they are close, but I am sure you can see what I mean:) These are the maxima, $(\frac{1}{2},\frac{\sqrt{3}}{2})$ and $(\frac{1}{2},-\frac{\sqrt{3}}{2})$. Professor McClure talked about "walking around the outside of the circle and coming upon the points of tangency". I am trying to think of it as the contours having to be outside of the restricted area up until the point of tangency, not inside like the first image.

These points come from the following calculations: $$\nabla f=<1,2y>$$
$$\nabla g=<2x,2y>$$
$$1=2\lambda x - solving for x=\frac{\lambda}{2}$$ $$2y=2\lambda y$$ here setting equal to zero $$ 2y-\lambda2y=0$$ $$2y(1-\lambda)=0$$ this gives us $$y=0$$ and $$\lambda = 1$$ Since$$x^2+y^2=1$$
Then for $y=0$ we know $x=-1$ based on our drawing. This gives us the minima at (-1,0). Now to consider
$$x=1/2\lambda$$
Since $\lambda = 1, x=\frac{1}{2}$
Making
$$y=\pm \sqrt {3/4}$$
Giving us the points:
$$(1/2,\sqrt {3/4)}$$
$$(1/2,-\sqrt {3/4)}$$.
 | 5 | No.5 Revision |
I actually missed this one on the exam, but since then have worked on what the contour diagram would look like. This should help along with what Professor McClure said in class.
(I am very much a beginner with Mathematica) But, if you can find your points on the circle, $(\frac{1}{2}, {\frac{\sqrt{3}}{2}})$ and $(\frac{1}{2}, -{\frac{\sqrt{3}}{2}})$, those points are where a contour would be tangent to the circle. Those are both maxima because as your contours move to the right, your function is set to a larger and larger constant. Likewise, looking on the left you can see a point of tangency where y=0. That is a minima, (-1,0).

This is a basic explanation and hopefully someone else will have more to add.
COMMENT ADDED After playing around with Mathematica I have generated another image that may help with the confusion. If you look at the previous image, the point of tangency at (1,0) is not a maximum. If you look at the new one below, you can see two points of tangency on the top and bottom of the circle (well, they are close, but I am sure you can see what I mean:) These are the maxima, $(\frac{1}{2},\frac{\sqrt{3}}{2})$ and $(\frac{1}{2},-\frac{\sqrt{3}}{2})$. Professor McClure talked about "walking around the outside of the circle and coming upon the points of tangency". I am trying to think of it as the contours having to be outside of the restricted area up until the point of tangency, not inside like the first image.

These points come from the following calculations: $$\nabla f=<1,2y>$$
$$\nabla g=<2x,2y>$$
$$1=2\lambda x - $$
solving for x=\frac{\lambda}{2}$$
$$x=\frac{1}{\lambda2}$$
Now the y components $$2y=2\lambda y$$ here setting equal to zero $$ 2y-\lambda2y=0$$ $$2y(1-\lambda)=0$$ this gives us $$y=0$$ and $$\lambda = 1$$ Since$$x^2+y^2=1$$
Then for $y=0$ we know $x=-1$ based on our drawing. This gives us the minima at (-1,0). Now to consider
$$x=1/2\lambda$$ Since $\lambda = 1, x=\frac{1}{2}$ Making $$y=\pm \sqrt {3/4}$$ Giving us the points: $$(1/2,\frac{\sqrt {3}}{2})$$ $$(1/2,-\frac{\sqrt {3}}{2})$$.
 | 6 | No.6 Revision |
I actually missed this one on the exam, but since then have worked on what the contour diagram would look like. This should help along with what Professor McClure said in class.
(I am very much a beginner with Mathematica) But, if you can find your points on the circle, $(\frac{1}{2}, {\frac{\sqrt{3}}{2}})$ and $(\frac{1}{2}, -{\frac{\sqrt{3}}{2}})$, those points are where a contour would be tangent to the circle. Those are both maxima because as your contours move to the right, your function is set to a larger and larger constant. Likewise, looking on the left you can see a point of tangency where y=0. That is a minima, (-1,0).

This is a basic explanation and hopefully someone else will have more to add.
COMMENT ADDED After playing around with Mathematica I have generated another image that may help with the confusion. If you look at the previous image, the point of tangency at (1,0) is not a maximum. If you look at the new one below, you can see two points of tangency on the top and bottom of the circle (well, they are close, but I am sure you can see what I mean:) These are the maxima, $(\frac{1}{2},\frac{\sqrt{3}}{2})$ and $(\frac{1}{2},-\frac{\sqrt{3}}{2})$. Professor McClure talked about "walking around the outside of the circle and coming upon the points of tangency". I am trying to think of it as the contours having to be outside of the restricted area up until the point of tangency, not inside like the first image.

These points come from the following calculations: $$\nabla f=<1,2y>$$
$$\nabla g=<2x,2y>$$ $$1=2\lambda x $$ solving for $$x=\frac{1}{\lambda2}$$
Now the y components
$$2y=2\lambda y$$
here setting equal to zero
y$$
$$ 2y-\lambda2y=0$$ $$2y(1-\lambda)=0$$ this gives us $$y=0$$ and $$\lambda = 1$$ Since$$x^2+y^2=1$$
Then for $y=0$ we know $x=-1$ based on our drawing. This gives us the minima at (-1,0). Now to consider
$$x=1/2\lambda$$ Since $\lambda = 1, x=\frac{1}{2}$ Making $$y=\pm \sqrt {3/4}$$ Giving us the points: $$(1/2,\frac{\sqrt {3}}{2})$$ $$(1/2,-\frac{\sqrt {3}}{2})$$.
