Revision history [back]

I'll take a stab at answering this, although I admit that I missed this on the exam as well! Here is what the question boils down to:

Use the method of Lagrange multipliers to find the extremes of $f(x, y) = x + y^2$ subject to the constraint $x^2 + y^2 = 1$.

To solve this problem, I will let $g(x, y) = x^2 + y^2$. Therefore:

$$\nabla f = \langle 1, 2y \rangle $$ $$\nabla g = \langle 2x, 2y \rangle $$

I will now set $\nabla f = \lambda \nabla g$. Two vectors are equal if and only if their components are equal. I will also add in the constraint curve to this system of equations so we will have a system of three equations in three variables (i.e. we can solve it).

$$ 1 = 2\lambda x $$ $$ 2y = 2\lambda y $$ $$ x^2 + y^2 = 1$$

Solving for $x$ in our first equation yields $x = \frac{1}{2\lambda}$. The second equation is a bit tricky to solve for $y$. You have to think about it for a second, since you cannot just divide by $y$ on both sides (or something similar). In this equation, $y$ must equal $0$ or $\lambda$ must equal $1$. I will examine both of these possibilities, but for now let us just consider the case where $y = 0$. Here is what our third equation looks like in this case:

$$\left(\frac{1}{2\lambda}\right)^2 + 0^2 = 1$$ $$\frac{1}{4\lambda^2} = 1$$ $$4\lambda^2 = 1$$ $$\lambda^2 = \frac{1}{4}$$ $$\lambda = \pm \frac{1}{2}$$

In the case of a negative lambda:

$$x = \frac{1}{2 * \left(-\frac{1}{2}\right)} = -1 $$ $$ y = 0 $$

Note that $y$ is independent of $x$ and $\lambda$ and is always equal to zero in this case.

In the case of a negative lambda:

$$x = \frac{1}{2 * \left(\frac{1}{2}\right)} = 1 $$ $$ y = 0 $$

This means that our extremes so far are $(-1, 0)$ and $(1, 0)$. However, we have not considered the case where $\lambda = 1$. If $\lambda = 1$, then:

$$x = \frac{1}{2 * 1} = \frac{1}{2}.$$

Here is what our third equation looks like in the case of $\lambda = 1$:

$$ \left(\frac{1}{2}\right)^2 + y^2 = 1$$

Solving for $y$ yields:

$$ \frac{1}{4} + y^2 = 1$$ $$ y^2 = 1 - \frac{1}{4} $$ $$ y^2 = \frac{3}{4} $$ $$ y = \pm \frac{\sqrt{3}}{2} $$

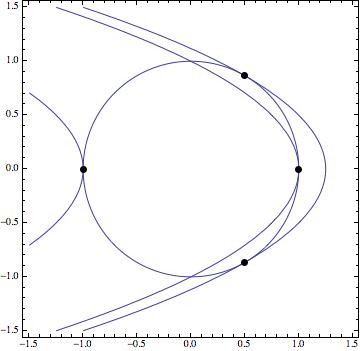
Therefore our four extremes are $(-1, 0)$, $(1, 0)$, $(\frac{1}{2}, -\frac{\sqrt{3}}{2})$, and $(\frac{1}{2}, \frac{\sqrt{3}}{2})$. If we take a look at our contour plot, we can see that the maximums occur at $(\frac{1}{2}, -\frac{\sqrt{3}}{2})$ and $(\frac{1}{2}, \frac{\sqrt{3}}{2})$.

I'll take a stab at answering this, although I admit that I missed this on the exam as well! Here is what the question boils down to:

Use the method of Lagrange multipliers to find the extremes of $f(x, y) = x + y^2$ subject to the constraint $x^2 + y^2 = 1$.

To solve this problem, I will let $g(x, y) = x^2 + y^2$. Therefore:

$$\nabla f = \langle 1, 2y \rangle $$ $$\nabla g = \langle 2x, 2y \rangle $$

I will now set $\nabla f = \lambda \nabla g$. Two vectors are equal if and only if their components are equal. I will also add in the constraint curve to this system of equations so we will have a system of three equations in three variables (i.e. we can solve it).

$$ 1 = 2\lambda x $$ $$ 2y = 2\lambda y $$ $$ x^2 + y^2 = 1$$

Solving for $x$ in our first equation yields $x = \frac{1}{2\lambda}$. The second equation is a bit tricky to solve for $y$. You have to think about it for a second, since you cannot just divide by $y$ on both sides (or something similar). In this equation, $y$ must equal $0$ or $\lambda$ must equal $1$. I will examine both of these possibilities, but for now let us just consider the case where $y = 0$. Here is what our third equation looks like in this case:

$$\left(\frac{1}{2\lambda}\right)^2 + 0^2 = 1$$ $$\frac{1}{4\lambda^2} = 1$$ $$4\lambda^2 = 1$$ $$\lambda^2 = \frac{1}{4}$$ $$\lambda = \pm \frac{1}{2}$$

In the case of a negative lambda:

$$x = \frac{1}{2 * \left(-\frac{1}{2}\right)} = -1 $$ $$ y = 0 $$

Note that $y$ is independent of $x$ and $\lambda$ and is always equal to zero in this case.

In the case of a negative positive lambda:

$$x = \frac{1}{2 * \left(\frac{1}{2}\right)} = 1 $$ $$ y = 0 $$

This means that our extremes so far are $(-1, 0)$ and $(1, 0)$. However, we have not considered the case where $\lambda = 1$. If $\lambda = 1$, then:

$$x = \frac{1}{2 * 1} = \frac{1}{2}.$$

Here is what our third equation looks like in the case of $\lambda = 1$:

$$ \left(\frac{1}{2}\right)^2 + y^2 = 1$$

Solving for $y$ yields:

$$ \frac{1}{4} + y^2 = 1$$ $$ y^2 = 1 - \frac{1}{4} $$ $$ y^2 = \frac{3}{4} $$ $$ y = \pm \frac{\sqrt{3}}{2} $$

Therefore our four extremes are $(-1, 0)$, $(1, 0)$, $(\frac{1}{2}, -\frac{\sqrt{3}}{2})$, and $(\frac{1}{2}, \frac{\sqrt{3}}{2})$. If we take a look at our contour plot, we can see that the maximums occur at $(\frac{1}{2}, -\frac{\sqrt{3}}{2})$ and $(\frac{1}{2}, \frac{\sqrt{3}}{2})$.

I'll take a stab at answering this, although I admit that I missed this on the exam as well! Here is what the question boils down to:

Use the method of Lagrange multipliers to find the extremes of $f(x, y) = x + y^2$ subject to the constraint $x^2 + y^2 = 1$.

To solve this problem, I will let $g(x, y) = x^2 + y^2$. Therefore:

$$\nabla f = \langle 1, 2y \rangle $$ $$\nabla g = \langle 2x, 2y \rangle $$

I will now set $\nabla f = \lambda \nabla g$. Two vectors are equal if and only if their components are equal. I will also add in the constraint curve to this system of equations so we will have a system of three equations in three variables (i.e. we can solve it).

$$ 1 = 2\lambda x $$ $$ 2y = 2\lambda y $$ $$ x^2 + y^2 = 1$$

Solving for $x$ in our first equation yields $x = \frac{1}{2\lambda}$. The second equation is a bit tricky to solve for $y$. You have to think about it for a second, since you cannot just divide by $y$ on both sides (or something similar). In this equation, $y$ must equal $0$ or $\lambda$ must equal $1$. I will examine both of these possibilities, but for now let us just consider the case where $y = 0$. Here is what our third equation looks like in this case:

$$\left(\frac{1}{2\lambda}\right)^2 + 0^2 = 1$$ $$\frac{1}{4\lambda^2} = 1$$ $$4\lambda^2 = 1$$ $$\lambda^2 = \frac{1}{4}$$ $$\lambda = \pm \frac{1}{2}$$

In the case of a negative lambda:

$$x = \frac{1}{2 * \left(-\frac{1}{2}\right)} = -1 $$ $$ y = 0 $$

Note that $y$ is independent of $x$ and $\lambda$ and is always equal to zero in this case.

In the case of a positive lambda:

$$x = \frac{1}{2 * \left(\frac{1}{2}\right)} = 1 $$ $$ y = 0 $$

This means that our extremes so far are $(-1, 0)$ and $(1, 0)$. However, we have not considered the case where $\lambda = 1$. If $\lambda = 1$, then:

$$x = \frac{1}{2 * 1} = \frac{1}{2}.$$

Here is what our third equation looks like in the case of $\lambda = 1$:

$$ \left(\frac{1}{2}\right)^2 + y^2 = 1$$

Solving for $y$ yields:

$$ \frac{1}{4} + y^2 = 1$$ $$ y^2 = 1 - \frac{1}{4} $$ $$ y^2 = \frac{3}{4} $$ $$ y = \pm \frac{\sqrt{3}}{2} $$

Therefore our four extremes are $(-1, 0)$, $(1, 0)$, $(\frac{1}{2}, -\frac{\sqrt{3}}{2})$, and $(\frac{1}{2}, \frac{\sqrt{3}}{2})$. If we take a look at our contour plot, we can see that the maximums occur at $(\frac{1}{2}, -\frac{\sqrt{3}}{2})$ and $(\frac{1}{2}, \frac{\sqrt{3}}{2})$.