-
Eigenranking
My matrix:[
[0, 4, 2, 2, 1],
[1, 0, 4, 4, 1],
[1, 3, 0, 4, 4],
[1, 3, 2, 0, 1],
[2, 1, 4, 1, 0]
]
Team 3: rating = 0.5317387251068555 Team 2: rating = 0.4743664736534873 Team 1: rating = 0.43963279846587106 Team 5: rating = 0.41258201033241837 Team 4: rating = 0.3587888852214044
Clearly, team 3 has the advantage. However, since this is bling archery, you can never tell who will pull out on top.
-
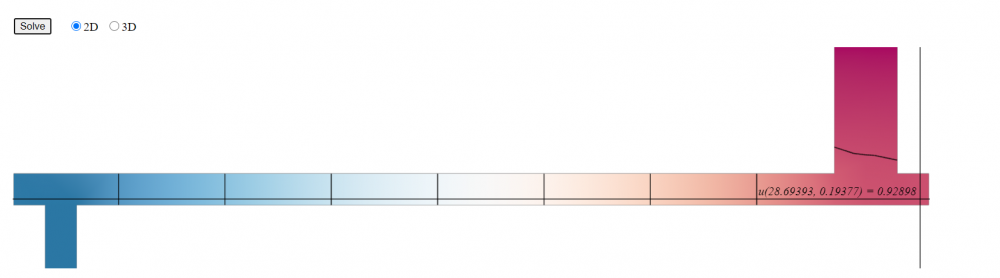
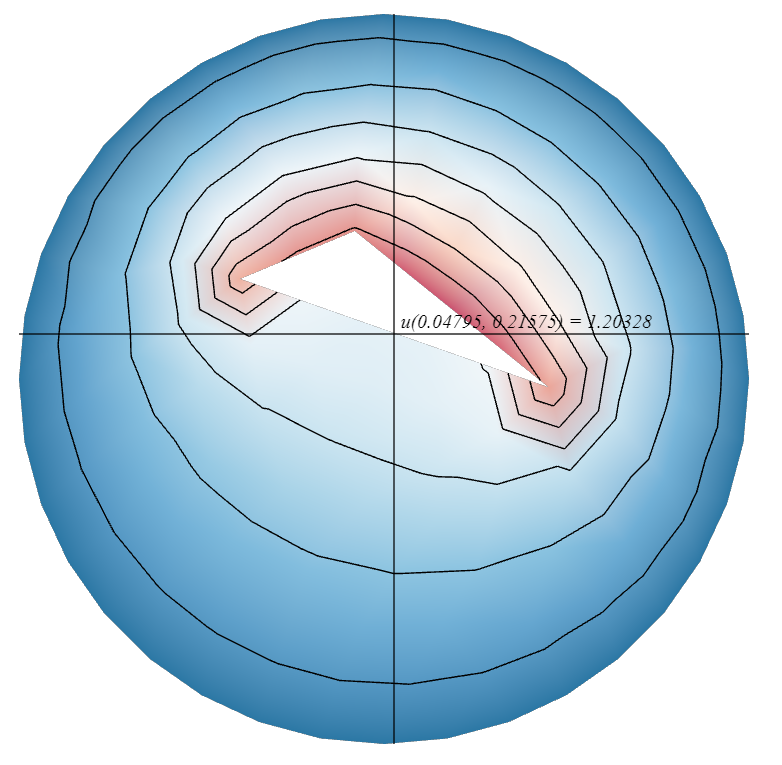
Modeling a steady state heat distribution in 2D
-
Modeling 2D Heat Flow
-
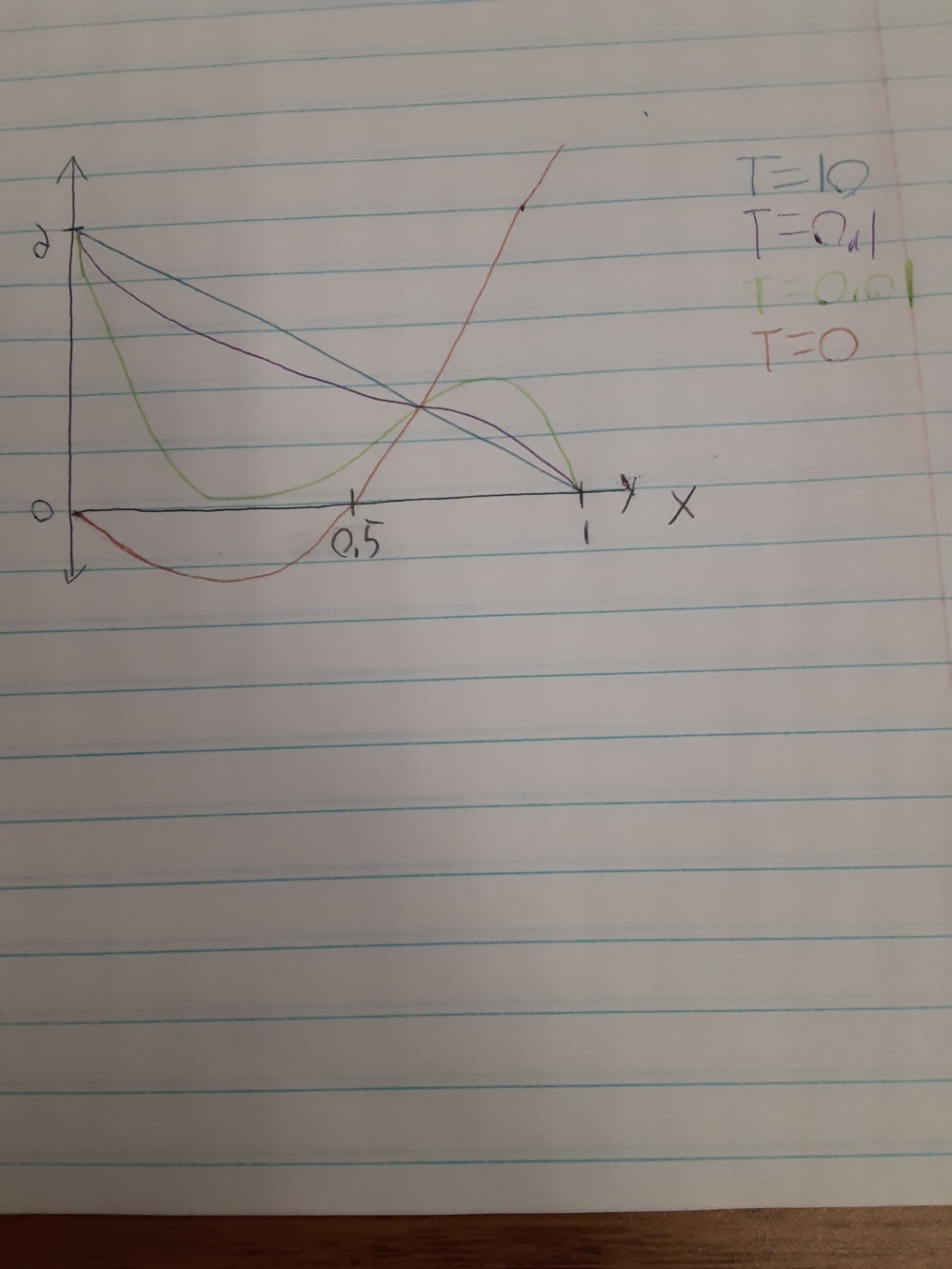
Random heat evolution problem
-
Steady state heat flow with source
Heat flow with a constant internal heat source is governed by:
$u_t=2u_{xx}+7$, $u(0,t)=−2$, $u(1,t)=4$.
Because this is a steady state temperature distribution, $u_t=0$ since $u(x,t)$ does not change with time. So,
$0=2u_{xx}+7$
Solving for $u_{xx}$ gives $u_{xx}=\frac{-7}{2}$. By integrating this equation twice we get:
$u(x,t)=\frac{-7}{4}x^2+c_1x+c_2$,
where $c_1$ and $c_2$ are our two constants. Solving for $c_1$ and $c_2$ using the initial conditions of $u(0,t)=-2$, $u(1,t)=4$ produces the steady state distribution of
$u(x,t)=\frac{-7}{4}x^2+\frac{3}{2}x+\frac{19}{4}$