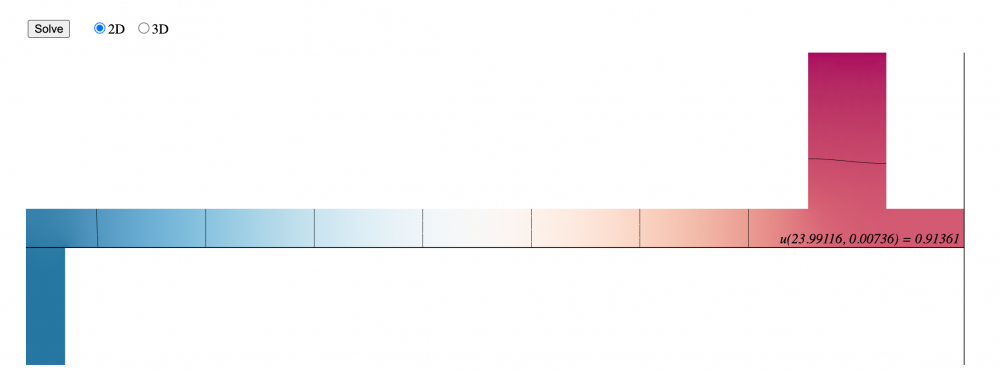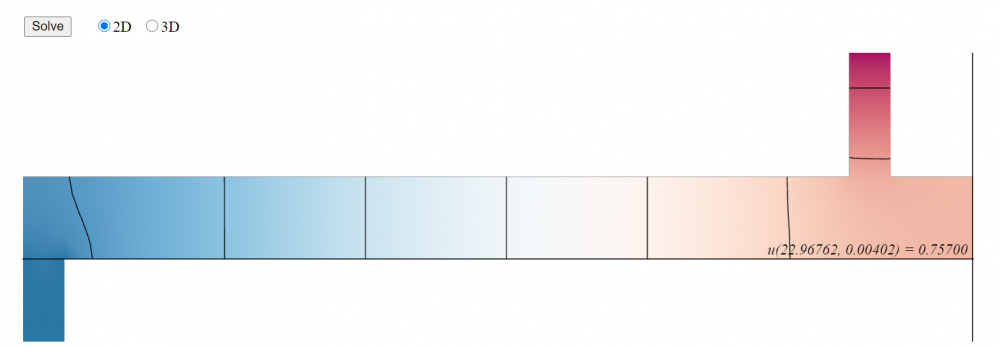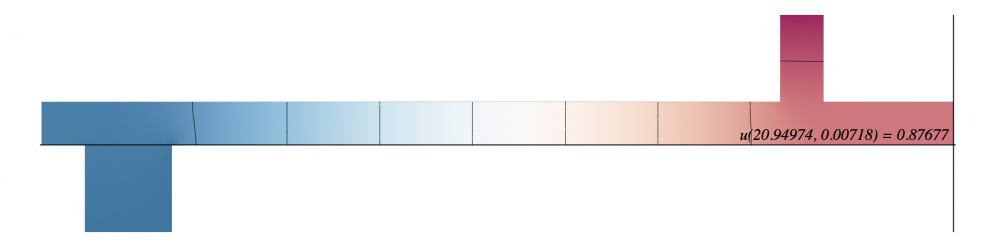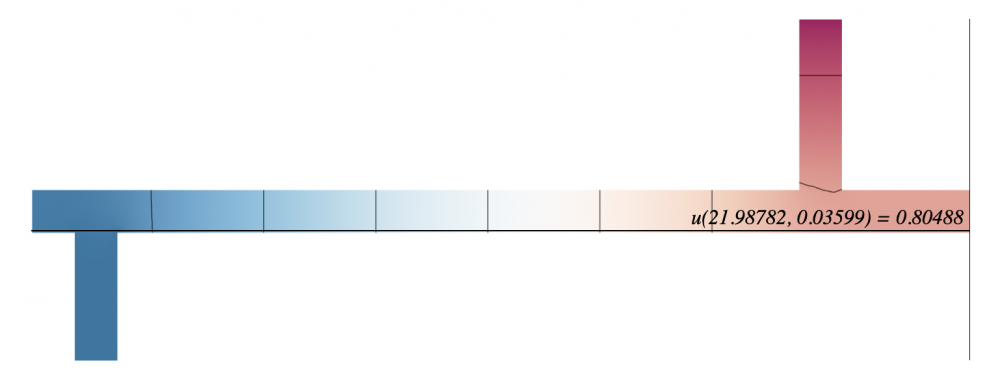Best Awesome Content
-
Eigenranking
My matrix was:
matrix = [
[0,3,3,3,1],
[2,0,3,1,3],
[3,3,0,3,1],
[4,1,1,0,4],
[1,1,3,4,0]
]
and the eigen ranking was:
Team 3: rating = 0.4627375562956863 Team 1: rating = 0.46273755629568625 Team 4: rating = 0.46088857575916814 Team 5: rating = 0.4269598459305646 Team 2: rating = 0.4207551766581456
Team 3 is barely ahead of team 1 by rounding. But otherwise these two teams are dead even for the best team.
-
Steady state heat flow with source
Heat flow with a constant internal heat source is governed by:
$u_t=2u_{xx}+7$, $u(0,t)=−2$, $u(1,t)=4$.
Because this is a steady state temperature distribution, $u_t=0$ since $u(x,t)$ does not change with time. So,
$0=2u_{xx}+7$
Solving for $u_{xx}$ gives $u_{xx}=\frac{-7}{2}$. By integrating this equation twice we get:
$u(x,t)=\frac{-7}{4}x^2+c_1x+c_2$,
where $c_1$ and $c_2$ are our two constants. Solving for $c_1$ and $c_2$ using the initial conditions of $u(0,t)=-2$, $u(1,t)=4$ produces the steady state distribution of
$u(x,t)=\frac{-7}{4}x^2+\frac{3}{2}x+\frac{19}{4}$
-
Steady state heat flow with source
Heat flow with a constant internal heat source is governed by $u_t = 3u_{xx} + 3$, $u(0,t) = -4$, $u(1,t) = 5$ Find the steady state temp distribution.
Set $u_t = 0$ which yields $u_{xx} = -1$ ; Integrating twice I get :
$u(x,t) = \frac{-1}{2}x^2 + \alpha(t)x + \beta(t)$
where $\alpha$ and $\beta$ are the two constants. Solving for our initial conditions, the steady state temp distribution function is
$u(x,t) = \frac{-1}{2}x^2 + 9.5x - 4$
-
Steady state heat flow with source
Heat flow with a constant internal heat source is governed by the following model:
$$u_t = 4u_{xx} + 5$$
Find the steady-state temperature distribution $u(x,t)$ if the boundary conditions are:
$$u( 0, t) = -2; u( 1, t) = 4$$
Steady-state implies that nothing changes with time, therefore:
$$\frac{du}{dt} = 0$$
Plugging the result into the model and rearranging the terms:
$$u_{xx} = - \frac{5}{4}$$
Integrate twice:
$$u_x = - \frac{5}{4} x + \phi (t)$$
$$u = - \frac{5}{8} x^2 + \phi (t)x + \psi (t)$$
Use boundary conditions to determine the unknown functions $\phi (t)$ and $\psi (t)$
$$u(0, t) = \psi (t) = -2$$
$$u(1, t) = -\frac{5}{8} + \phi (t) + (-2) = 4 \rightarrow \phi(t) = \frac{53}{8}$$
Therefore, the steady state temperature distribution is:
$$\boxed{u(x,t) = - 0.625 x^2 + 9.6 x -2}$$
-
Steady state heat flow with source
We will look at heat flow with a constant internal heat source. This will be governed by, $$u_t=4{u_xx}+8.$$
Such that we have the initial conditions, $u(0,t)=-3$ and $u(1,t)=3.$
Given that we are looking for a steady-state distribution, we can set $u_t=0,$ such that $u(x,t)$ does not change with respect to time, $t.$
Therefore, we have the equation $$0=4{u_xx}+8.$$
Simplifying we get:
$$4{u_xx}=-8$$
$${u_xx}=-2.$$
Integrating twice we get
$${u_x}=-2x+{c_1}$$
$$u=-x^{2}+x{c_1}+{c_2}.$$
Using our initial conditions, we will solve for $c_1$ and $c_2$:
We get ${c_1}=7$ and ${c_2}=-3.$
Thus, our steady-state distribution function is:
$$u=-x^2+7x-3.$$
-
Steady state heat flow with source
Heat flow with a constant internal heat source is governed by
$$u_t = 3u_{xx} + 4\ ; \ u(0,t) = 1, \ u(1,t) = 2$$
Find the steady state temperature distribution.
Steady state: $u_t = 3u_{xx} + 4 = 0 \ \longrightarrow \ u_{xx} = -\frac{4}{3}$
$$u = \int\int -\frac{4}{3}\ dx = -\frac{2}{3}x^2 + c_{1}x + c_2$$
Initial conditions:
$u(0,t) = 1 \ \longrightarrow \ c_2 = 1$
$u(1,t) = 2 \ \longrightarrow \ -\frac{2}{3} + c_1 + 1 = 2 \ \longrightarrow \ c_1 = \frac{5}{3}$
So, $\boxed{u(x,t) = -\frac{2}{3}x^2 + x + \frac{5}{3}}$
-
Modeling a steady state heat distribution in 2D
The temperature in the lower right hand corner of the bar at steady state is roughly 0.91361.
-
Modeling a steady state heat distribution in 2D
Given the conditions of my problem with $\kappa=0$ and $f=0$ the temperature at the lower right hand corner of the bar at steady state is 0.75700.
-
Modeling a steady state heat distribution in 2D
With my unique conditions I formed a polygon where $\kappa=0$ and $f=0$, meaning there was no external heat source present and no signs of growth/decay. After reaching steady state the temperature in the lower right hand corner of the polygon was $u=0.87677$.
-
Modeling a steady state heat distribution in 2D
For my unique conditions, $\kappa = 0$ and $f = 0$. The three sides on the lower left, sticking out of the bar, are set to temperature zero. The side at the very top of the rectangle on the upper right is set to temperature 1. The remaining sides are insulated. At the steady state for the heat distribution, the temperature for the lower right corner of the bar is $u = 0.80488$.
