Your basins of attraction

mark

Use the mm/dd/yy form of your birthday to create a polynomial. For example, my birthday is 08/04/64, so my polynomial is
[dmath]
f(x) = 8 x + 4 x^3 + 6 x^4 + 4 x^5.
[/dmath]

Then,

1. Find the roots of your polynomial, and
2. Use our complex Newton's method tool to generate the basins of attraction.

theoldernoah

My polynomial is
[dmath] f(x) = 8x + 6x^3 + 9x^4 + 6x^5. [/dmath]

The roots for my polynomial are:

[dmath] x={-1.1221 - 0.863761i, -1.1221 + 0.863761i, 0, 0.3721 - 0.725592i, 0.3721 + 0.725592i} [/dmath]

And finally my basins of attraction are:

Sampson

My polynomial is:

[dmath] 5x+2x^2+2x^3+9x^4+6x^5 [/dmath]

The roots that ground me are:

[dmath] x= 1., 0.703704, 0.428406, 0.166214, 0.0161617, 0.000106813 [/dmath]

My basins of attraction are the following:

Callie

My polynomial is:
[dmath] x+2x^2+4x^3+9x^4+6x^5 [/dmath]
The roots of my polynomial are:
[dmath]x =-1, -0.643493, 0, 0.0717464 - 0.503841i, 0.0717464 + 0.503841i [/dmath]
My basins of attraction look like this:

Lorentz

My polynomial is
[dmath]
4 x +2 x^{2} + 6x^{3} + 9x^{4} + 6x^{5}
[/dmath]

The roots to this polynomial are
[dmath]
x = {-0.9713 - 0.6569i,
-0.9713 + 0.6569i,
0.2213 - 0.6602i,
0.221 + 0.6602i}
[/dmath]

Nick

My polynomial is
[dmath]
f(x) = x+5x^3+9x^4+6x^5
[/dmath]

The roots of the polynomial are
[dmath]
x= -0.86999-0.585147i, -0.86999+0.585147i, 0, 0.11999-0.370428i, 0.11999+0.370428i
[/dmath]

SomeCallMeTim

My polynomial is [dmath] f_{tim}(z)=1+8z^3+8z^4+z^5[/dmath]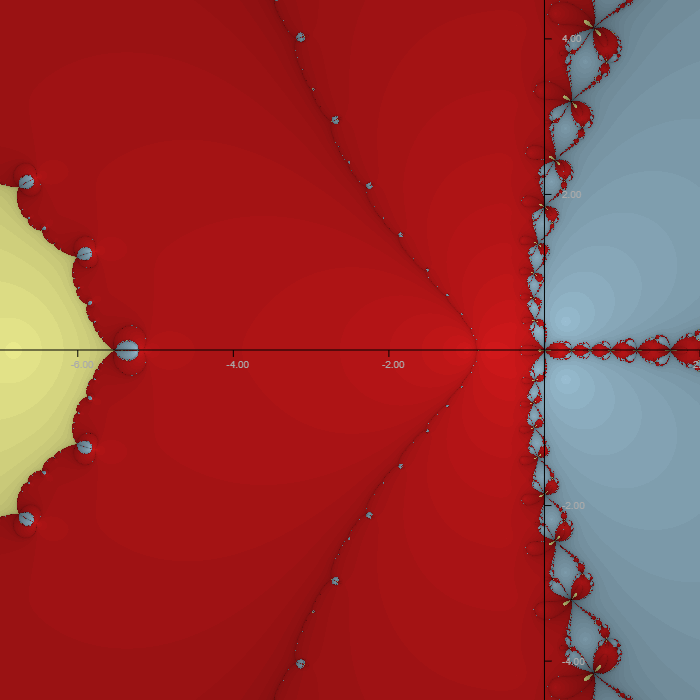
This function has real roots located at [imath] z= -0.704432, z= -1, z= -6.828982[/imath], as well as complex roots at [imath] z=0.26771 \pm .36979 i. [/imath] My birthday has a lot of zeroes in it, as well as a different birth year than many of you, which seems to produce a very different looking graph.

Here's another view, this time in a square 1000 by 1000 window centered about the origin.

Cornelius

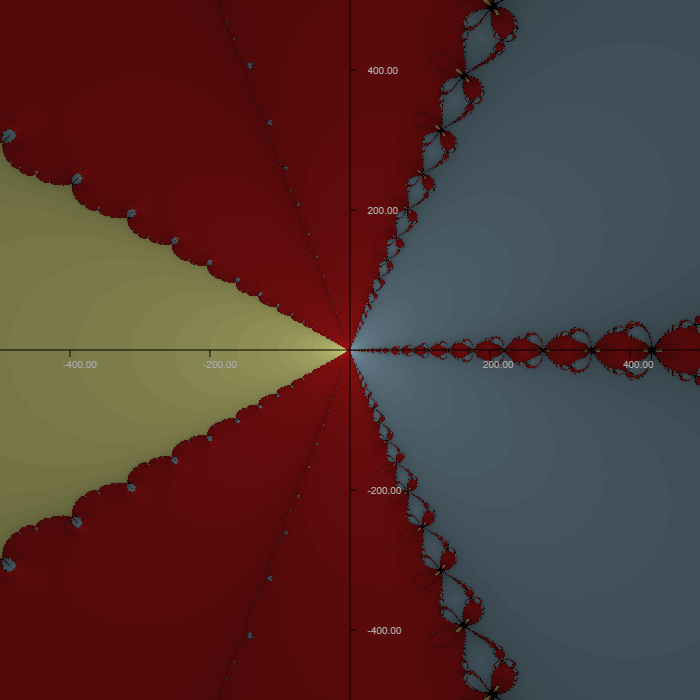
My polynomial is:

[dmath]
f(x) = x^2+4x^3+9x^4+4x^5
[/dmath]

The roots of the polynomial are:

[dmath]
x = -1.76328, -0.243358 + 0.287329i, -0.243358 - 0.287329i
[/dmath]

My basins of attractions are:

aisling

My Birthday polynomial is
[dmath]
1+x+x^3+9x^4+3x^5.
[/dmath]
The roots of my polynomial are
[dmath]
x=2.8749, -0.4532\pm 0.3407i, 0.39073\pm 4.5597i.
[/dmath]
My basins of attraction graph:

SighHillDoveN

Birthday Polynomial:

[dmath]
f(x)=3z+17z^2+9z^3+6z^4
[/dmath]

Roots of Birthday Polynomial:

[dmath]
-0.679697\pm.757008i, 0.236462\pm0.450628i
[/dmath]

Basins of Attraction:

breezyFbaby

My birthday is 05/01/96, so my polynomial is
[dmath]
f(x)=5+x^2+9x^3+6x^4.
[/dmath]

The roots for this polynomial is:
[dmath]
-1.16129-0.43049i, -1.16129+.43049i, 0.41129-0.61164i, 0.41129+0.61164i
[/dmath]

the basins of attraction is:

joezayatz

My birthday is 12/06/95, so my polynomial looks like
[dmath]
f(x) = 1 + 2x + 6x^3 + 9x^4 + 5x^5
[/dmath]

The roots for this polynomial are:
[dmath]
x = -0.39851, 0.3016 + 0.48895i, 0.3016 - 0.48895i, -1.00234 + 0.71832, -1.00234 - 0.71832
[/dmath]

Basins of attraction:

maththemagician

My Birthday is 06/11/96
My Function is: [dmath]
6 x + x^2 + x^3 + 9 x^4 + 6 x^5
[/dmath]
My Roots are:{{x -> -1.18088 - 0.408791 I}, {x -> -1.18088 + 0.408791 I}, {x ->
0.}, {x -> 0.430885 - 0.67432 I}, {x -> 0.430885 + 0.67432 I}}

eric

eric

for f(z) = 4 + z + z^2 + z^3 + 9 z^4 == 0, z.
the roots for this one are;
{z -> -0.581341 - 0.558751 I}, {z -> -0.581341 + 0.558751 I},
{z -> 0.525785 - 0.638077 I}, {z -> 0.525785 + 0.638077 I}}

I really didn't like my dinky little fractal so I made this one.

eric

eric

For 4 z + z^2 + z^3 + 9 z^4
the roots are
{{z -> -0.751062}, {z -> 0.}, {z -> 0.319976 - 0.69955 I},
{z -> 0.319976 + 0.69955 I}}

eric

For f(z) =4 + z + z^2 + z^3 + 9 z^4.
{{z -> -0.581341 - 0.558751 I}, {z -> -0.581341 + 0.558751 I},
{z -> 0.525785 - 0.638077 I}, {z -> 0.525785 + 0.638077 I}}.

I liked this modified version better, (mine looked really dinky.)

Rex

Hi!

My polynomial is

[dmath]
f(z) = 4+z+9z^{2}+8z^{3}+4z^{4}
[/dmath]

The roots of my polynomial come out to be:

[imath]
{z\to -1.},{z\to 0.0836872\, -0.632981 i},{z\to 0.0836872\, +0.632981 i},{z\to 0.416313\, -1.50985 i},{z\to 0.416313\, +1.50985 i}
[/imath]