Best Recent Content

  • Your personal fractal spiral

    Rex Rex

    My personal dimension using my name, Rex is

    $$d = 1.18524$$

    I let my $r0 = 0.97$

    plugging into mathematica:

    s = 1.18524;
    r0 = 0.97;
    Solve[r0^s + r1^s == 1, r1]
    {{r1 -> 0.05975492237886343}}

    Using the IFS visualizer with the following settings:

    r0 = 0.97;
    r1 = 0.0597549;
    t = 22*degree;
    [
    rotate(t).compose(scale(r0)),
    scale(r1,[1,0])
    ]

    Gives me this:

    mark

  • Your personal fractal spiral

    Sampson Sampson

    Using my full first name "Samuel" produces the fractal dimension:

    [dmath] d=1.1911321512 [/dmath]

    Using [imath] r=.95 [/imath] yeilds the following equation:

    [dmath] {.95}^{1.1911321512} + {r_1}^{1.1911321512} = 1 [/dmath]

    I then solved for [imath] r_1 [/imath] using the Mathematica solve function yielding:

    [dmath] r_1 = 0.093269 [/dmath]

    I wanted my fractal to look a little different so I used [imath]t=5.221996 [/imath] in the IFS visualizer which is of the form MM.DDYYYY. This yielded the following:

    mark

  • Your personal fractal spiral

    maththemagician maththemagician

    Using my last name which is Tittle gives me the fractal dimension
    [dmath] d=0.1.2092020125[/dmath]

    Using [dmath] r_0= .9 [/dmath]

    and the equation [dmath] r_0^d+r_1^d=1

    the result from mathematica is {{r -> 0.172724}} for r_1

    I used this value in the IFS generator with 11 degrees of freedom to produce

    mark

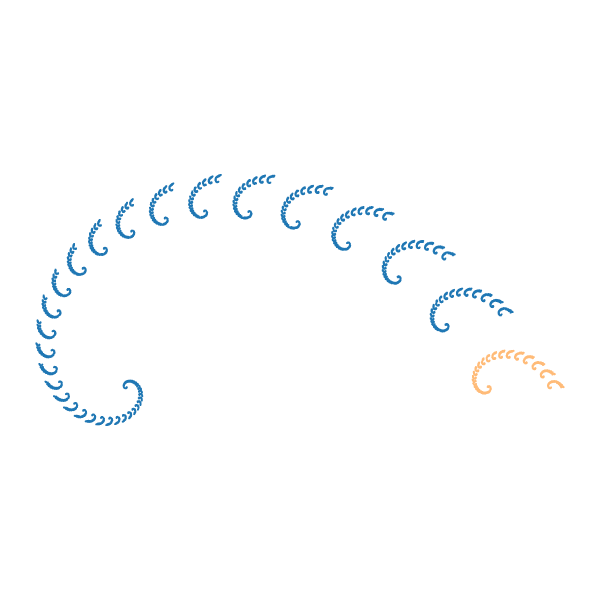
  • Your personal fractal spiral

    breezyFbaby breezyFbaby

    My personal dimension using my first name, Bronaza, is [dmath]
    d=1.21815141261
    [/dmath].

    I let my $r_0=.96$.
    So, using my $r_0$ and my $d$, I substituted it into the following formula to solve for $r_1$ on mathematica.
    [dmath]r_0^d+r_1^d=1[/dmath]

    The output is [dmath]r_1=.083404[/dmath].

    So using the IFS visualizer and choosing the spiral IFS and selecting a random degree of $266.4444$. I got the code:

    r0 = 0.96;
    r1 = 0.083404;
    t = 266.4444*degree;
    [
    rotate(t).compose(scale(r0)),
    scale(r1,[1,0])
    ]

    which generated the following image:

    mark

  • A plane self-similar set of dimension e-1

    theoldernoah theoldernoah

    Our dimension is [imath] e-1 [/imath]. We will choose an arbitrary large value [imath] r_0=0.99 [/imath] and solve the equation:

    [dmath] 0.99^{e-1} + r^{e-1}=1 [/dmath]

    Which gives us [imath] r \approx 0.0937498 [/imath] after plugging it into Mathematica.

    We then plug these two [imath] r [/imath] values into our IFS visualizer, under spiral, and get the following:

    r0 = 0.99;
    r1 = 0.0937498;
    t = 15*degree;
    [
    rotate(t).compose(scale(r0)),
    scale(r1,[1,0])
    ]

    mark

  • Your personal fractal spiral

    eric eric

    Erik maps to 5,18,9,11 = 1.518911, so i used
    FindRoot[$(.93)^{1.518911}+(r)^{1.518911}$==1, {r,1}]
    which equals r= .225873 

     r0 = 0.93;
 r1 = 0.225873;
 t = 40*degree;
 [
  rotate(t).compose(scale(r0)),
  scale(r1,[1,0])
  ]
    mark

  • Your personal fractal spiral

    Jon Jon

    My first name is Jonathan so the dimension of my fractal is 1.1015141208114.
    The value of r = 0.89 was chosen for no reason and the rotation degree was chosen randomly.
    The Mathematica code to generate my spiral using the fractal geometry package:

    d = 1.1015141208114;
    r = 0.89 ;
    Solve[r^d + r1^d == 1, r1]

    {{r1 -> 0.146411}}

    birthdaySpiralIFS = {
    {0.89 RotationMatrix[RandomReal[{1, 180}]], {0, 0}},
    { 0.146411 IdentityMatrix[2], {1, 0}}
    };
    ShowIFSStochastic[birthdaySpiralIFS, 80000, Colors -> True]

    mark

  • Your personal fractal spiral

    Nick Nick

    My personal dimension using my full first name Nicholas is
    [dmath]
    d = 1.149381512119
    [/dmath]

    I chose $r_0 = .88$ and then plugged it into the following equation:
    [dmath]
    r_0^d+r_1^d = 1
    [/dmath]

    Then using some Mathematica code, I solved the above equation for $r_1$

    d = 1.149381512119;
    r0 = 0.96;
    Solve[r0^d + r1^d == 1, r1]
    r1 -> 0.176986

    so $r_1 = 0.176986$

    I then chose t to have the value of 33 (because it's my favorite number and this is my personal fractal spiral) and used the following code for the IFS Visualizer

    r0 = 0.88;
    r1 = 0.176986;
    t = 33*degree;
    [
    rotate(t).compose(scale(r0)),
    scale(r1,[1,0])
    ]

    And the code output the following fractal spiral

    mark

  • Your personal fractal spiral

    joezayatz joezayatz

    Using my full first name Joseph, my dimension is equivalent to
    [dmath]
    d = 1.1015195168
    [/dmath]
    I chose [dmath] r_0 = 0.91 [/dmath] and the equation [dmath] r_0^d + r_1^d = 1 [/dmath] to produce [dmath] r_1 = 0.122149 [/dmath] using some Mathematica code. I then used the following code in the IFS Visualizer:
    r0 = 0.91;
    r1 = 0.122149;
    t = 70*degree;
    [
    rotate(t).compose(scale(r0)),
    scale(r1,[1,0])
    ]

    to produce my personal fractal spiral:

    mark

  • Box-counting dimension for a self-affine set

    Lorentz Lorentz

    There are four functions each one operates with the same contraction ratios with the last three shifting the contracted vector within the unit square. Since they are shifted up and to the right by a multiple of the width and height you end up with four distinct rectangles the second iterations acts upon this new set of points which creates four new copies and so on.

    Each rectangle can be broken in two squares of side length [dmath] \frac{1}{4} [/dmath] which leaves you with [dmath] 8^n [/dmath] squares. Therefore our convergent sequence and number of squares is

    [dmath]
    \epsilon = \frac{1}{4}^n
    N_{\epsilon}=8^n
    [/dmath]

    [dmath]
    dim(E)=\frac{\log(8^n)}{\log(4^n)}=1.5
    [/dmath]

    mark