Login info:
This forum is invite only. To register your account, follow the invite link in your invitation email.
Your favorite function
What is your favorite function? Enter it in nice, typeset mathematics and plot it, together with the line [imath]y=x[/imath].

Comments
My favorite function is the same as my Dad's! It's:
[dmath]
f(x) = e^{-x^2}.
[/dmath]
The graph looks like this:
Ayy my favorite function is:
[dmath]
f(x)=e^{ix}
[/dmath]
My beloved function is for the Lorentz factor because it is so useful for my favorite frame of reference.
[dmath]
\gamma = \frac{1}{\sqrt{1- \frac{v^2}{c^2}}}
[/dmath]
https://www.desmos.com/calculator/qgilurylz6
My favorite function is:
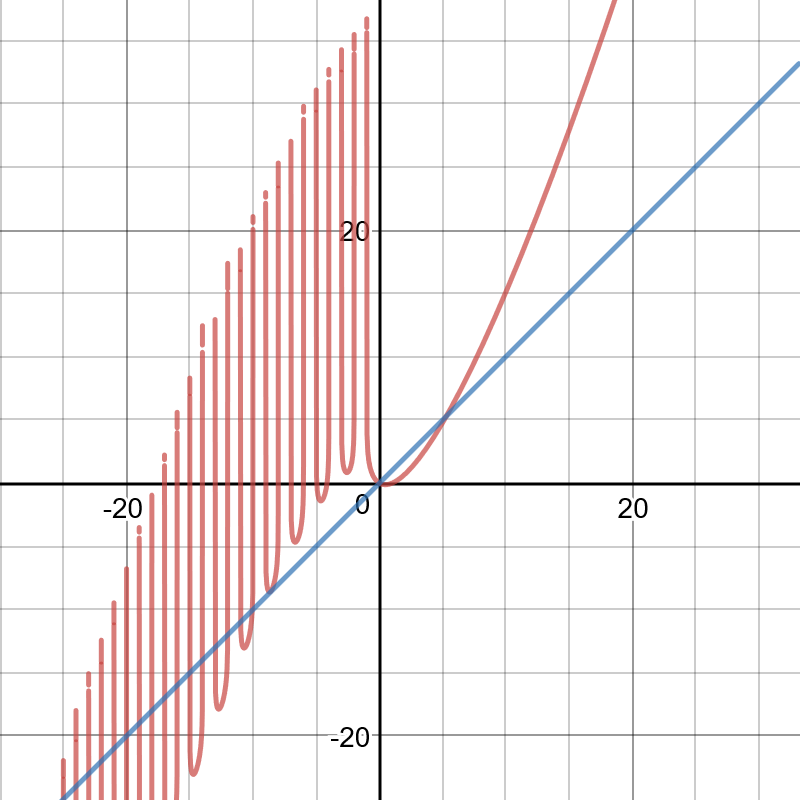
[dmath]
y=\ln (n!)
[/dmath]
My favorite function is:
[dmath]
f(x)=\sin(x+f(x))
[/dmath]
The graph looks like this: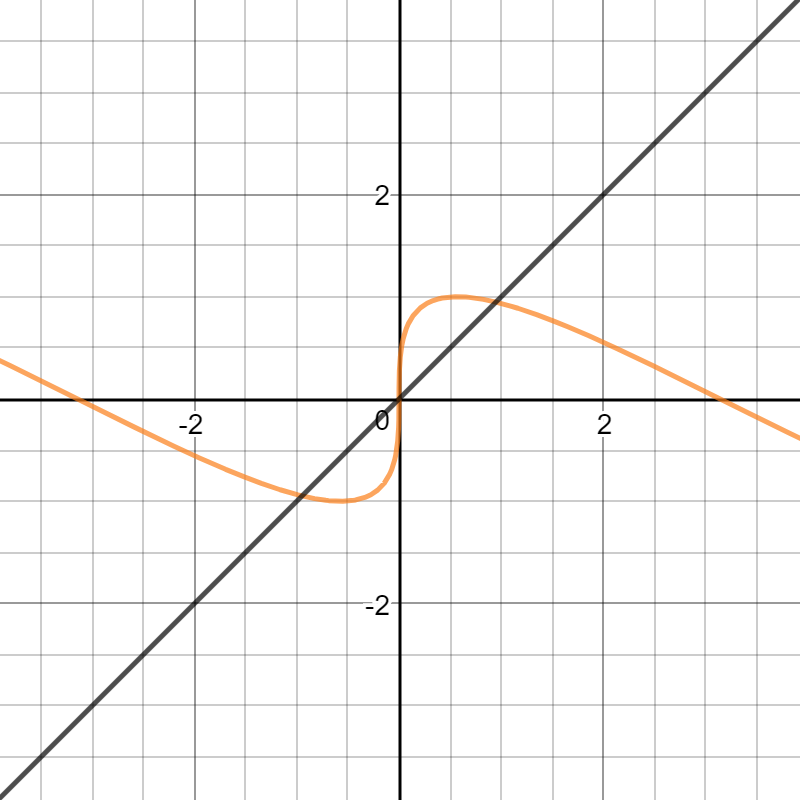
My favorite function is just the natural exponential function is the humble natural exponential function, solely for the reason that its derivative is itself.
[dmath]
f(x) = e ^ x
[/dmath]
The graph looks like this: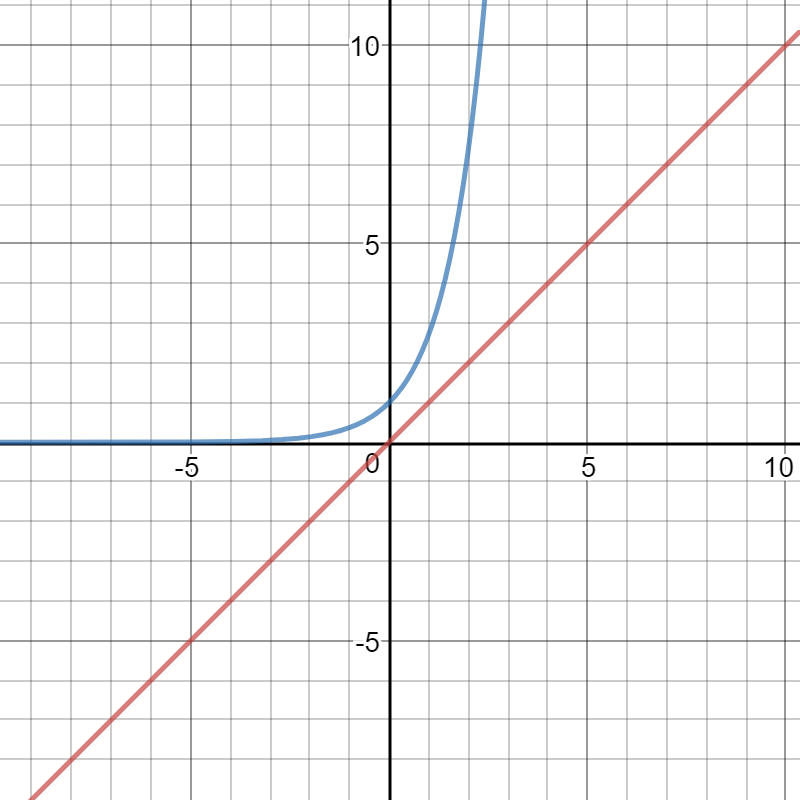
My favorite function is [dmath]f(x)=\sin \frac{1}{x}.[/dmath] The rate of oscillations increase without bound as x approaches zero, which results in the neat springy shape seen in the linked image.
My favorite function is
[dmath]
f(x)=x^3.
[/dmath]
The graph to this function looks like this:
https://www.desmos.com/calculator/lmavj1l9ib
My favorite function is
[dmath]
f(x) = sin(x) + x
[/dmath]
The graph to this function looks like this:
https://www.desmos.com/calculator/ohk5s6uvah
One of my favorite functions is:
[dmath] r =2sin(8.5theta) [/dmath]
where the coefficient of theta can be changed to create all kinds of beautiful flowers!
Graph: https://www.desmos.com/calculator/jbpa4gdxms
My favorite function is:
[dmath] f(x)=cos(3x+3)! [/dmath]
The graph looks like really long teeth!
Graph:
Lately I have been very fond of this function:
[dmath] f(x)=3sin(ln(θ^{2}+1)) [/dmath]
Here is what it looks like:
[dmath]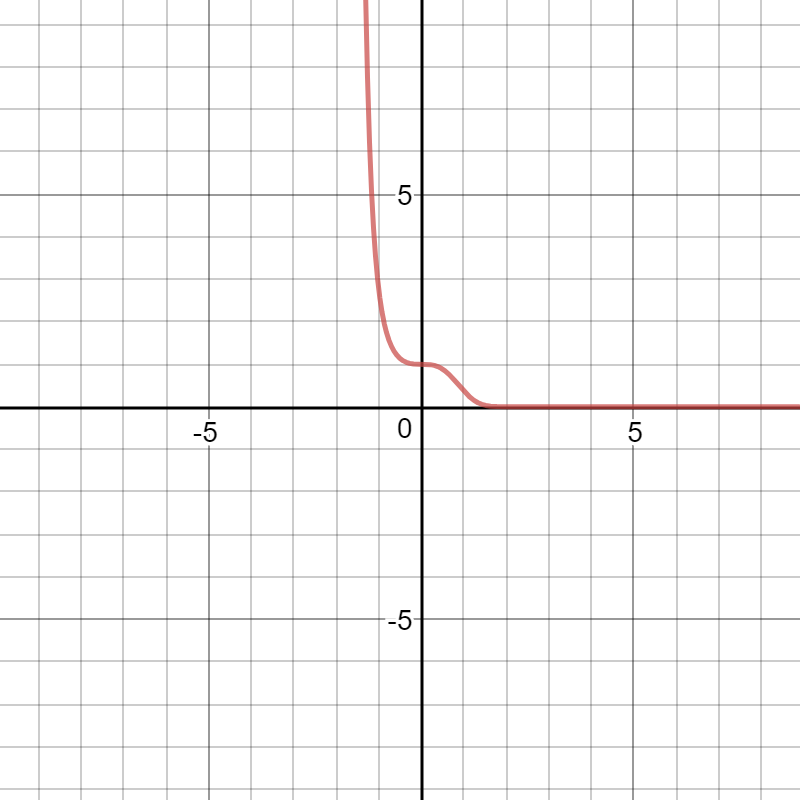
f(x)=e^{-x^3}
[/dmath]
* It looks like this! I find it to be an accurate indicator for my GPA throughout the semester with respect to time!
*
My favorite function is
[dmath]
f(x) = x^{2}
[/dmath]
specifically in relation to its derivative, 2x. "Calculus" is a word that conjures up great fear in the general public. It's uttered in hushed tones and is often met with a grave silence while those who hear it respond with the stone faced seriousness of a soldier re-living the horrors of war. But if you can look at x^2 and decide that for your own purposes that you want it to be 2x now, you're doing calculus. Easy!
This is what it looks like:
A function I like is:
[dmath]f(x) = \log(x)+\sin(x^{3})[/dmath]