Box-counting dimension for a self-affine set

mark

Consider the following IFS of four Affine functions:

[dmath]
\begin{align}
f_1(\vec{x}) &= \left(
\begin{array}{cc}
\frac{1}{4} & 0 \\
0 & \frac{1}{2}
\end{array}
\right) \cdot \vec{x} \\
f_2(\vec{x}) &= \left(
\begin{array}{cc}
\frac{1}{4} & 0 \\
0 & \frac{1}{2}
\end{array}
\right) \cdot \vec{x} + \left(
\begin{array}{c}
\frac{1}{4} \\
\frac{1}{2} \
\end{array}
\right)\\
f_3(\vec{x}) &= \left(
\begin{array}{cc}
\frac{1}{4} & 0 \\
0 & \frac{1}{2}
\end{array}
\right) \cdot \vec{x} + \left(
\begin{array}{c}
\frac{1}{2} \\
0
\end{array}
\right) \\
f_4(\vec{x}) &= \left(
\begin{array}{cc}
\frac{1}{4} & 0 \\
0 & \frac{1}{2}
\end{array}
\right) \cdot \vec{x} + \left(
\begin{array}{c}
\frac{3}{4} \\
\frac{1}{2}
\end{array}
\right)
\end{align}
[/dmath]

Several iterations of this IFS applied to the unit square are shown below:

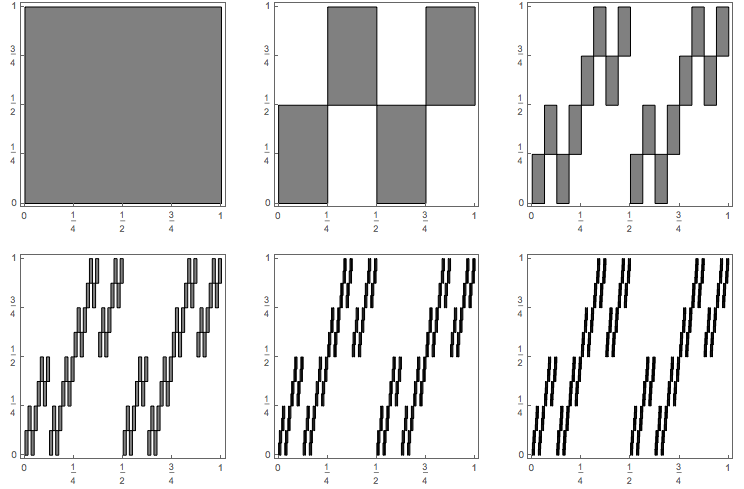
In particular, note that the image of the square is not another square - it's a rectangle that's twice as tall as it is wide. After 5 steps away from the square, we see a good approximation to the limiting attractor, which we denote $E$.

• Show that $n^{\text{th}}$ cover of $E$ generated by this process consists of $4^n$ rectangles of width $1/4^n$ and height $1/2^n$.
• How many squares of side length $1/4^n$ must each of the rectangles in the previous part be decomposed into to cover the attractor with squares?
• Use the squares from the previous part to compute $N_{4^{-k}}(E)$. Don't count squares that intersect $E$ only in their boundaries.
• Compute the box counting dimension of $E$.

Lorentz

There are four functions each one operates with the same contraction ratios with the last three shifting the contracted vector within the unit square. Since they are shifted up and to the right by a multiple of the width and height you end up with four distinct rectangles the second iterations acts upon this new set of points which creates four new copies and so on.

Each rectangle can be broken in two squares of side length [dmath] \frac{1}{4} [/dmath] which leaves you with [dmath] 8^n [/dmath] squares. Therefore our convergent sequence and number of squares is

[dmath]
\epsilon = \frac{1}{4}^n
N_{\epsilon}=8^n
[/dmath]

[dmath]
dim(E)=\frac{\log(8^n)}{\log(4^n)}=1.5
[/dmath]

Lorentz

The number of squares needed to cover each rectangle is 2 that would mean

[dmath]
N_{\frac{1}{4^n}}=2 * 4^n
[/dmath]
[dmath]
dim (E)= \lim_{n \rightarrow \infty} \frac{\log(2)+\log(4^n)}{log(4^n)}=1
[/dmath]