Just even periods

mark

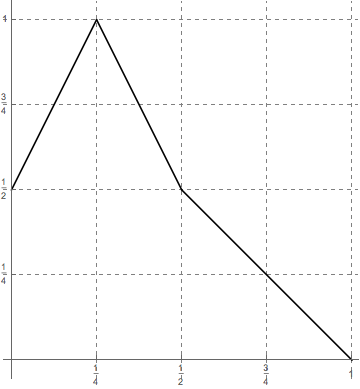
Show that the function [imath]f:[0,1]\to[0,1][/imath] whose graph is shown below has orbits of all even periods but no orbits of any odd period (other than the fixed point at [imath]1/2[/imath]). How does this example fit into the Sharkovsky order?

SomeCallMeTim

We note that for [imath] x \in [0,\frac{1}{2}),f(x)\in [\frac{1}{2},1][/imath], and that for [imath]x \in (\frac{1}{2},1], f(x)\in [0,\frac{1}{2})[/imath] We further note that [imath]f(\frac{1}{2})=\frac{1}{2}[/imath], so [imath]\frac{1}{2}[/imath] is a fixed point of [imath]f[/imath].

Let us define [imath]A=[0,\frac{1}{2}), B=(\frac{1}{2},1][/imath]. Let [imath]x_0[/imath] be a periodic point of an orbit with period [imath]n[/imath].

Without loss of generality, if we assume that [imath]x_0 \in A[/imath], then after any odd number [imath]j[/imath] steps of iteration, [imath]x_j \in B[/imath], and after any even number of steps we "land" in somewhere in the interval A.

Since the period [imath]n[/imath] of an orbit is defined by the minimum number of iterations of [imath]x_0[/imath] by [imath]f[/imath] such that [imath]f^n(x_0)=x_0[/imath], and [imath]f^n(x_0)\in A[/imath] is only true if [imath]n[/imath] is even, [imath]n[/imath] must be an even number, thus there cannot exist any odd periodic orbits of [imath]f[/imath].

Now that we know there are not any odd periodic orbits, we would like to know more about which even periodic orbits exist. According to Sharkovsky's theorem, [imath]3\cdot 2 \triangleleft x \forall[/imath]even [imath]x[/imath]. This means that if we can find a period 6 orbit, we can conclude that [imath]f[/imath] must have periodic orbits for all even periods.

We turn to Mathematica for assistance. In the following code, we define our function, and plot in the desired range to confirm a match to our original graph.

f[x_] = Piecewise[{{1/2 + 2 x, 0 <= x <= 1/4}, {3/2 - 2 x, 
1/4 < x <= 1/2}, {1 - x, 1/2 < x <= 1}}]
Plot[f[x], {x, 0, 1}]

We solve for points which are of period 6:

x /. Solve[f[f[f[f[f[f[x]]]]]] == x, x]

Which gives us the following candidate points:

{1/18, 1/14, 1/6, 3/14, 5/18, 5/14, 7/18, 1/2, 11/18, 9/14, 13/18, 
11/14, 5/6, 13/14, 17/18}

We test and confirm the point 1/18 is of period 6 under iteration of [imath]f[/imath].

NestList[f, 1/18, 6]
{1/18, 11/18, 7/18, 13/18, 5/18, 17/18, 1/18}

Since we have located an orbit of period 6, by Sharkovsky's theorem, there must exist periods of all even orbits. Since we have also shown that there cannot exist any odd period orbits for this function, we conclude that [imath]f[/imath] has orbits of all even periods but no orbits of any odd period.