Final exam review: Test 1
Hey everyone, I think it's a good time for us to start reviewing things for the final. It is a short class after all and it'll be here before we know it. I think it's a good idea for us to use ask bot as a data base for important assignments, tests and quizzes. Creating these posts is a great way for the reviewer to review an assignment and if we all chip in and post explanations of these things on the website than we'll have a very complete resource for anything we could want to go over. I'll start by covering test 1.
Note: Completing these takes a serious amount of time. It's conceivable that two people could be working on the same assignment at the same time. So before completing one of these reviews leave an answer to this question explaining what you will cover so we can get through it in the most efficient way possible. When your post goes up use the tag I've used on this post, "DataBase" so we can have them all in one location.
1)
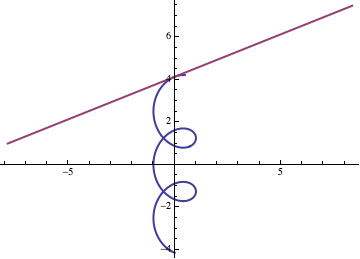
"An object moves according to the parametrization $p(t)= \langle - \cos (5t), \sin(5t) +2t \rangle$."
A) Describe the motion determined by $p(t)$.
You can make the motion described by this path more apparent by breaking it into the sum of two vectors. $$p(t)= \langle - \cos(5t), \sin(5t) \rangle+ \langle0, 2t \rangle$$
The first vector in this sum describes clockwise circular motion. We know it is circular motion because the $\cos(5t)$ term and the $ \sin(5t)$ term both have the same coefficient, $1$. We know it is clockwise because the $\cos(5t)$ term is negative, which tells us that it moves from negative $-1$ to $1$ over the interval $[0, \pi]$. The second vector describes linear motion along the positive $y$ axis. So we can conclude that this is a clockwise circular path that travels "up" along the positive $y$ axis. Here's a groovy picture.

B) Write down a parametrization of the line tangent to the path at the point when $t= \frac{\pi}{2}$
To parametrize this line, we use the formula $l(t)= p_{0}+dt$ where $p_{0}$ is a point along the line and $d$ is a direction vector for the line.
First we find $p_{0}$, which is the point on the circular path where $t= \frac{\pi}{2}$. To find it all we have to do is plug this value into $p(t)$. $$p_{0}= \langle -\cos(\frac{5 \pi}{2}),\sin(\frac{5 \pi}{2})+\pi \rangle$$ $$= \langle 0,1+\pi \rangle$$
Next we find $d$. This direction vector can be found by plugging in our value of $t$ into $p'(t)$. $$p'(t)= \langle 5 \sin(5t),5 \cos(5t)+2 \rangle$$ $$d= p'(\frac{\pi}{2})= \langle 5 \sin(\frac{5 \pi}{2}),5 \cos(\frac{5 \pi}{2}+2 \rangle$$ $$= \langle 5, 2 \rangle$$
Now we have everything we need to create our parametrization. $$l(t)= \langle 0,1+ \pi \rangle + \langle 5,2 \rangle t$$ $$= \langle 5t,2t+1+\pi \rangle$$
Here's another groovy picture.
C) "Write down an integral representing the distance traveled by the object over the time interval $0$ to $3 \pi$."
We use the formula $D= \int_{a}^{b} ||p'(t)||dt$ to answer this question and recall from part B that $$p'(t)= \langle 5 \sin(5t),5 \cos(5t)+2 \rangle$$
The magnitude of $p'(t)$ is the square root of the sum of the squares of the components. Or $$||p'(t)||=[25 \sin^{2}(5t)+(25 \cos(5t)+2)^{2}]^{\frac{1}{2}}$$
So our integral is
$$D= \int_{0}^{3 \pi}[25 \sin^{2}(5t)+(25 \cos(5t)+2)^{2}]^{\frac{1}{2}}dt$$
2)
"Let $v= \langle 1,-2,3 \rangle$ and let $w= \langle -1,1,3 \rangle$. Find $proj_{v}w$, the vector projection of $w$ onto $v$".
So remember that the formula for the projection of $w$ onto $v$ is $$proj_{v}w= \frac{v \cdot w}{|v|^{2}}v$$ $$=\frac{\langle 1,-2,3 \rangle \cdot \langle -1,1,3 \rangle}{1^{2}+2^{2}+3^{2}} \langle 1,-2,3 \rangle$$ $$= \frac{3}{7} \langle 1,-2,3 \rangle$$
3)
"Find all values of $t$ so that $ \langle 1,-t,-t^{2} \rangle$ is perpendicular to $ \langle 1,1,1 \rangle$."
The given vector will be perpendicular to $ \langle 1,1,1 \rangle$ at all values of $t$ such that the dot product of the two vectors is equal to zero. $$\langle 1,-t,-t^{2}\rangle \cdot \langle 1,1,1 \rangle =1-t-t^{2}$$
The quadratic formula is then used to find the values of t such that this expression is zero. $$\frac{1 \pm [1-(4)(-1)(1)]^{\frac{1}{2}}}{-2}=- \frac{1}{2} \pm \frac{5^{\frac{1}{2}}}{2}$$
4)
"Prove that the two dimensional dot product is commutative."
This means to prove $a \cdot b=b \cdot a$
This will be a component wise proof.
Let $a= \langle a_{1},a_{2} \rangle$ and $b= \langle b_{1},b_{2} \rangle$
Then $a \cdot b= \langle a_{1},a_{2} \rangle \cdot \langle b_{1},b_{2} \rangle$ $$=a_{1}b_{1}+a_{2}b_{2}$$ $$=b_{1}a_{1}+b_{2}a_{2}$$ $$= \langle b_{1},b_{2} \rangle \cdot \langle a_{1},a_{2} \rangle$$ $$= b \cdot a$$
5)
"Describe the motions determined by the following two parametrized paths. What is the relationship between the two motions?"
A) $p(t)= \langle 1,2,3 \rangle + \langle -2,2,-1 \rangle t$
B) $p(t)= \langle 1,2,3 \rangle + \langle -2,2,-1 \rangle \sin(t)$
A fits the formula for the parametrization of a line through the point $(1,2,3)$. B is a little more complicated. It also fits the formula for the parametrization of a line through the point $(1,2,3)$ but it has its direction vector multiplied by $sin(t)$ instead of $t$. From an intuitive perspective this may make it seem like this gives the line some sort of oscillating behavior, however, this simply means the speed that an object travels along this path oscillates. So this path is a line segment through the point $(1,2,3)$.
6)
"Find the equation of a plane that contains the points $(2,2,-1),(0,1,-1)$ and $(-2,3,-1)$. Or explain why no such plane exists."
This problem can be solved with no math whatsoever. All the points contain a $z$ coordinate of $-1$. So the plane containing them is $z=-1$.
7)
"Find the parametrization of the line through the point $(1,2,3)$ and perpendicular to the plane $2x-y+3z=6$."
To solve this problem we use the formula for the parametrization of a line given earlier $$l(t)= p_{0}+dt$$
We have been given the point $p_{0}$ so all we need is a normal vector to plug in everything to the formula. Recall that the components of the normal vector are the respective coefficients of the equation of the plane. This make the normal vector $d= \langle 2,-1,3 \rangle $.
So our line is $$l(t)= \langle 1,2,3 \rangle + \langle 2,-1,3 \rangle t$$
8)
"Parametrize the intersection between the sphere of radius $2$ centered at the point $(1,1,1)$ with the plane y=2"
First things first. Define your sphere. $$S=(x-1)^{2}+(y-1)^{2}+(z-1)^{2}$$
Next set $y$ equal to $2$ to find your intersection with the plane $y=2$. $$(x-1)^{2}+(z-1)^{2}=3$$
This equation describes a circle centered at $(1,0,1)$ with radius $3^{ \frac{1}{2}}$
Now we plug these values into the parametric equation of a circle.
$$p(t)=c+rv \cos(t) + ru \sin(t)$$ Where $c$ is the position vector of the center of the circle $r$ is the radius of the circle and $v$ and $u$ are two perpendicular unit vectors in the plane of the circle. In this case they can be the unit vectors $ \langle 1,0,0 \rangle$ and $ \langle 0,0,1 \rangle$.
The parametrized circle is $$ \langle 1,0,1 \rangle +3^{\frac{1}{2}} \langle 1,0,0 \rangle \cos(t) + 3^{\frac{1}{2}} \langle 0,0,1 \rangle \sin(t)$$
Another Groovy Picture!!

9)
"Let $f(x,y)=x^{2}-3y^{2}$. A) Compute $f(1,2)$ B) Compute $\frac{\partial f}{\partial x}$ and $\frac{\partial f}{\partial y}$.
I think we've all gotten really familiar with problems like these since this test so I'll just leave the correct answers.
A) $$f(1,2)=1-3(4)=-11$$
B) $$\frac{\partial f}{\partial x}=2x$$ $$\frac{\partial f}{\partial y}=-6y$$
10)
"Let $p(t)= \langle 1+3t,2+4t \rangle$ and let $q(t)= \langle 3-t,-4+3t \rangle$. A) Find the point of intersection between the paths parametrized by $p$ and $q$. B) Do the motions parametrized by $p$ and $q$ collide?"
To determine if the lines intersect set the components of each equal to each other. To make things easier use $t$ for the variable in one vector and $s$ for the other. $$1+3t=3-s$$ $$2+4t=3s-4$$
Solving the system shows us that $t=0$ and $s=2$. By plugging these values into their appropriate equations we see they both give the point $(1,2)$ as the location of intersection.
We know the paths do not collide even though they intersect because $s \neq t$.
