answered
2014-07-18 16:12:06 -0600
I don't remember the problem exactly, but I believe it went something like this:
Find all maxima of the function $ f(x, y) = (x^2-y^2)e^{-(x^2+y^2)}. $
Even if this is not the exact same problem, the concepts should still apply. The first thing I did was find both of the first derivatives.
$$ f_x = (2x)e^{-(x^2+y^2)} + (-2x)e^{-(x^2+y^2)}(x^2-y^2) $$
$$ f_x = (-2y)e^{-(x^2+y^2)} + (-2y)e^{-(x^2+y^2)}(x^2-y^2) $$
I then set them equal to zero:
$$ (2x)e^{-(x^2+y^2)} + (-2x)e^{-(x^2+y^2)}(x^2-y^2) = 0 $$
$$ (-2y)e^{-(x^2+y^2)} + (-2y)e^{-(x^2+y^2)}(x^2-y^2) = 0 $$
Factoring both of the equations results in:
$$ (2x)e^{-(x^2+y^2)}(1 - (x^2-y^2)) = 0 $$
$$ (-2y)e^{-(x^2+y^2)}(1+ (x^2-y^2)) = 0 $$
Since $e^{-(x^2+y^2)}$ never will equal $0$, I can divide both sides of both equations by it, yielding:
$$ (2x)(1 - (x^2-y^2)) = 0 $$
$$ (-2y)(1+ (x^2-y^2)) = 0 $$
With some simplifications, this is:
$$ (2x)(1 - x^2 + y^2) = 0 $$
$$ (-2y)(1 + x^2 - y^2) = 0 $$
Okay, so here is where the art of solving systems of equations comes into play. We know that the first equation is equal to zero when $2x = 0$. The solution to this equation is obviously $x = 0$. Plugging in $x = 0$ into the second equation yields:
$$ (-2y)(1 - y^2) = 0 $$
This means that either $-2y = 0$ or $1 - y^2 = 0$.
First possibility:
$$ -2y = 0 $$
$$ y = 0 $$
Second possibility:
$$ 1 - y^2 = 0 $$
$$ y^2 = 1 $$
$$ y = \pm 1 $$
I find it useful to think of a "tree" of values to keep track of this.
x = 0
|
+---- y = 0
|
+---- y = -1
|
+---- y = 1
We will now repeat this same process with $y$, since we know that the second will equal zero when $-2y = 0$. Again, this has an obvious solution: $y = 0$. Plugging in $y = 0$ into the first equation yields:
$$ (2x)(1 - x^2) = 0 $$
This means that either $2x = 0$ or $1 - x^2 = 0$.
First possibility:
$$ 2x = 0 $$
$$ x = 0 $$
Second possibility:
$$ 1 -x^2 = 0 $$
$$ x^2 = 1 $$
$$ x = \pm 1 $$
Let's add it to our wonderful tree of life!
+---- x = 0
| |
| +---- y = 0 -> (0, 0)
| |
| +---- y = -1 -> (0, -1)
| |
| +---- y = 1 -> (0, 1)
|
+---- y = 0
|
+---- x = 0 -> (0, 0)
|
+---- x = -1 -> (-1, 0)
|
+---- x = 1 -> (1, 0)
Removing any duplicates, we are left with the points: $(0, 0)$, $(0, -1)$, $(0, 1)$, $(-1, 0)$, $(1, 0)$.
An inspection of the contour plot (which was given on the exam) shows us that the maxima occur at $(-1, 0)$ and $(1, 0)$. Here is the contour plot for reference (courtesy of WolframAlpha).
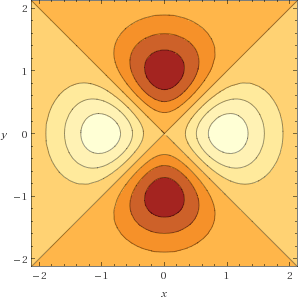
For what it's worth, this also tells us that minima occur at $(0, -1)$ and $(0, 1)$. This leaves $(0, 0)$, which the contour plot tells us is a saddle point.
Update/Comment
I completely agree with Kyouko and Christina. I too spent a long time worrying that it didn't line up, but then I realized what the caption to the graph said (the function didn't match up exactly with the problem).