Revision history [back]

I agree with Tiffany about everything except the radius and $\vec u$ and $\vec v$. Just for the sake of completion, I will go over all my steps.

The general equation for a parametrized circle is as follows:

$$ \vec p(t) = \vec c + r \cos(t) \vec u + r \sin(t) \vec v $$

The first piece of information that we must find is an equation describing the plane that the circle lies in. We do this by setting the equations of the spheres equal to each other. Since the radii are both equal to 1, we don't have to wrry about adding or subtracting constants.

$$ x^2 + y^2 + z^2 = (x-1)^2 + (y-1)^2 + (z-1)^2 $$ $$ x^2 + y^2 + z^2 = (x^2 - 2x + 1) + (y^2 - 2y + 1) + (z^2 - z + 1) $$

After rearranging the terms, we obtain:

$$ - 2x - 2y - 2z = -3 $$

This is the equation for our plane. This problem can now be thought of as the intersection of the unit sphere and this plane.

The next piece of information we need is the normal vector to the plane. This is easy!

$$ \vec n = \langle -2, -2, -2 \rangle $$

Now we can find $\vec u$ and $\vec v$. To find $\vec u$, I will choose a random vector that is perpendicular to $\vec n$ (i.e. one that lies on our plane).

$$ \vec u = \langle 0, 1, -1 \rangle $$

Note that $\vec n \cdot \vec u = 0$. We will now cross $\vec n$ with $\vec u$ to find a vector that is perpendicular to both of them.

$$ \vec v = \vec n \times \vec u = \langle 4, -2, -2 \rangle $$

Note that if you take the dot product between any of these two vectors, you will get $0$. Next, we must normalize these vectors (divide them by their magnitude).

$$ \vec u = \langle 0, 1, -1 \rangle / \sqrt{2} $$ $$ \vec v = \langle 4, -2, -2 \rangle / \sqrt{24} $$

Next we will find the center of this circle. The center of the circle must lie on our plane, so we will find when the line that has a direction vector as the normal of the plane intersects the plane. This point of intersection is our center. Note that in our line, $p_0 = \langle 0, 0, 0 \rangle$.

$$ \vec l(t) = \vec n t = \langle -2, -2, -2 \rangle t = \langle -2t, -2t, -2t \rangle $$

If we plug in the components of this vector into our plane, we will find the $t$ value of the intersection.

$$ -2 (-2t) - 2(-2t) - 2(-2t) = -3 $$ $$ 4t + 4t + 4t = -3 $$ $$ t = -\frac{1}{4} $$

We will now substitute in $-\frac{1}{4}$ for $t$ in our line.

$$\vec c = \vec l \left(-\frac{1}{4} \right) = \left\langle \frac{1}{2}, \frac{1}{2}, \frac{1}{2} \right\rangle $$

Now we have everything except the radius. I admit, I am completely drawing a blank on how to find the radius. I've thought about it for a while, but I just have no idea. Experimental evidence (Grapher app on Macs) has concluded that the radius is equal to $\frac{1}{2}$, but why? If someone could clarify, I would be so happy!

As it stands, here is our equation:

$$ \vec p(t) = \left\langle 1/2, 1/2, 1/2 \right\rangle + r\cos(t)\frac{\langle 0, 1, -1 \rangle}{\sqrt{2}} + r\sin(t)\frac{\langle 4, -2, -2 \rangle}{\sqrt{24}} $$

So if anyone knows how to find the radius... please let me know!

I agree with Tiffany about everything except the radius and $\vec u$ and $\vec v$. Just for the sake of completion, I will go over all my steps.

The general equation for a parametrized circle is as follows:

$$ \vec p(t) = \vec c + r \cos(t) \vec u + r \sin(t) \vec v $$

The first piece of information that we must find is an equation describing the plane that the circle lies in. We do this by setting the equations of the spheres equal to each other. Since the radii are both equal to 1, we don't have to wrry about adding or subtracting constants.

$$ x^2 + y^2 + z^2 = (x-1)^2 + (y-1)^2 + (z-1)^2 $$ $$ x^2 + y^2 + z^2 = (x^2 - 2x + 1) + (y^2 - 2y + 1) + (z^2 - z + 1) $$

After rearranging the terms, we obtain:

$$ - 2x - 2y - 2z = -3 $$

This is the equation for our plane. This problem can now be thought of as the intersection of the unit sphere and this plane.

The next piece of information we need is the normal vector to the plane. This is easy!

$$ \vec n = \langle -2, -2, -2 \rangle $$

Now we can find $\vec u$ and $\vec v$. To find $\vec u$, I will choose a random vector that is perpendicular to $\vec n$ (i.e. one that lies on our plane).

$$ \vec u = \langle 0, 1, -1 \rangle $$

Note that $\vec n \cdot \vec u = 0$. We will now cross $\vec n$ with $\vec u$ to find a vector that is perpendicular to both of them.

$$ \vec v = \vec n \times \vec u = \langle 4, -2, -2 \rangle $$

Note that if you take the dot product between any of these two vectors, you will get $0$. Next, we must normalize these vectors (divide them by their magnitude).

$$ \vec u = \langle 0, 1, -1 \rangle / \sqrt{2} $$ $$ \vec v = \langle 4, -2, -2 \rangle / \sqrt{24} $$

Next we will find the center of this circle. The center of the circle must lie on our plane, so we will find when the line that has a direction vector as the normal of the plane intersects the plane. This point of intersection is our center. Note that in our line, $p_0 = \langle 0, 0, 0 \rangle$.

$$ \vec l(t) = \vec n t = \langle -2, -2, -2 \rangle t = \langle -2t, -2t, -2t \rangle $$

If we plug in the components of this vector into our plane, we will find the $t$ value of the intersection.

$$ -2 (-2t) - 2(-2t) - 2(-2t) = -3 $$ $$ 4t + 4t + 4t = -3 $$ $$ t = -\frac{1}{4} $$

We will now substitute in $-\frac{1}{4}$ for $t$ in our line.

$$\vec c = \vec l \left(-\frac{1}{4} \right) = \left\langle \frac{1}{2}, \frac{1}{2}, \frac{1}{2} \right\rangle $$

Now we have everything except the radius. I admit, I am completely drawing a blank on how to find the radius. I've thought about it for a while, but I just have no idea. Experimental evidence (Grapher app on Macs) has concluded that the radius is equal to $\frac{1}{2}$, but why? If someone could clarify, I would be so happy!

As it stands, here is our equation:

$$ \vec p(t) = \left\langle 1/2, 1/2, 1/2 \frac{1}{2}, \frac{1}{2}, \frac{1}{2} \right\rangle + r\cos(t)\frac{\langle 0, 1, -1 \rangle}{\sqrt{2}} + r\sin(t)\frac{\langle 4, -2, -2 \rangle}{\sqrt{24}} $$

So if anyone knows how to find the radius... please let me know!

I agree with Tiffany about everything except the radius and $\vec u$ and $\vec v$. Just for the sake of completion, I will go over all my steps.

The general equation for a parametrized circle is as follows:

$$ \vec p(t) = \vec c + r \cos(t) \vec u + r \sin(t) \vec v $$

The first piece of information that we must find is an equation describing the plane that the circle lies in. We do this by setting the equations of the spheres equal to each other. Since the radii are both equal to 1, we don't have to wrry about adding or subtracting constants.

$$ x^2 + y^2 + z^2 = (x-1)^2 + (y-1)^2 + (z-1)^2 $$ $$ x^2 + y^2 + z^2 = (x^2 - 2x + 1) + (y^2 - 2y + 1) + (z^2 - z + 1) $$

After rearranging the terms, we obtain:

$$ - 2x - 2y - 2z = -3 $$

This is the equation for our plane. This problem can now be thought of as the intersection of the unit sphere and this plane.

The next piece of information we need is the normal vector to the plane. This is easy!

$$ \vec n = \langle -2, -2, -2 \rangle $$

Now we can find $\vec u$ and $\vec v$. To find $\vec u$, I will choose a random vector that is perpendicular to $\vec n$ (i.e. one that lies on our plane).

$$ \vec u = \langle 0, 1, -1 \rangle $$

Note that $\vec n \cdot \vec u = 0$. We will now cross $\vec n$ with $\vec u$ to find a vector that is perpendicular to both of them.

$$ \vec v = \vec n \times \vec u = \langle 4, -2, -2 \rangle $$

Note that if you take the dot product between any of these two vectors, you will get $0$. Next, we must normalize these vectors (divide them by their magnitude).

$$ \vec u = \langle 0, 1, -1 \rangle / \sqrt{2} $$ $$ \vec v = \langle 4, -2, -2 \rangle / \sqrt{24} $$

Next we will find the center of this circle. The center of the circle must lie on our plane, so we will find when the line that has a direction vector as the normal of the plane intersects the plane. This point of intersection is our center. Note that in our line, $p_0 = \langle 0, 0, 0 \rangle$.

$$ \vec l(t) = \vec n t = \langle -2, -2, -2 \rangle t = \langle -2t, -2t, -2t \rangle $$

If we plug in the components of this vector into our plane, we will find the $t$ value of the intersection.

$$ -2 (-2t) - 2(-2t) - 2(-2t) = -3 $$ $$ 4t + 4t + 4t = -3 $$ $$ t = -\frac{1}{4} $$

We will now substitute in $-\frac{1}{4}$ for $t$ in our line.

$$\vec c = \vec l \left(-\frac{1}{4} \right) = \left\langle \frac{1}{2}, \frac{1}{2}, \frac{1}{2} \right\rangle $$

Now we have everything except the radius. I admit, I am completely drawing a blank on how to find the radius. I've thought about it for a while, but I just have no idea. Experimental evidence (Grapher app on Macs) has concluded that the radius is equal to $\frac{1}{2}$, but why? If someone could clarify, I would be so happy!

This is the circle with a radius of $0.5$:

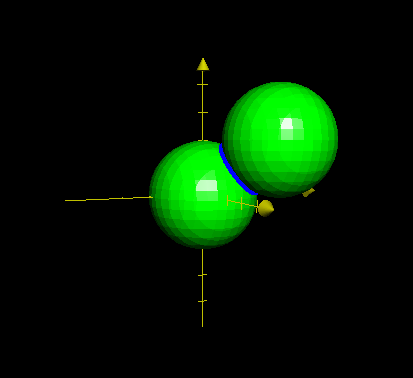
As it stands, here is our equation:

$$ \vec p(t) = \left\langle \frac{1}{2}, \frac{1}{2}, \frac{1}{2} \right\rangle + r\cos(t)\frac{\langle 0, 1, -1 \rangle}{\sqrt{2}} + r\sin(t)\frac{\langle 4, -2, -2 \rangle}{\sqrt{24}} $$

So if anyone knows how to find the radius... please let me know!

I agree with Tiffany about everything except the radius and $\vec u$ and $\vec v$. Just for the sake of completion, I will go over all my steps.

The general equation for a parametrized circle is as follows:

$$ \vec p(t) = \vec c + r \cos(t) \vec u + r \sin(t) \vec v $$

The first piece of information that we must find is an equation describing the plane that the circle lies in. We do this by setting the equations of the spheres equal to each other. Since the radii are both equal to 1, we don't have to wrry about adding or subtracting constants.

$$ x^2 + y^2 + z^2 = (x-1)^2 + (y-1)^2 + (z-1)^2 $$ $$ x^2 + y^2 + z^2 = (x^2 - 2x + 1) + (y^2 - 2y + 1) + (z^2 - z + 1) $$

After rearranging the terms, we obtain:

$$ - 2x - 2y - 2z = -3 $$

This is the equation for our plane. This problem can now be thought of as the intersection of the unit sphere and this plane.

The next piece of information we need is the normal vector to the plane. This is easy!

$$ \vec n = \langle -2, -2, -2 \rangle $$

Now we can find $\vec u$ and $\vec v$. To find $\vec u$, I will choose a random vector that is perpendicular to $\vec n$ (i.e. one that lies on our plane).

$$ \vec u = \langle 0, 1, -1 \rangle $$

Note that $\vec n \cdot \vec u = 0$. We will now cross $\vec n$ with $\vec u$ to find a vector that is perpendicular to both of them.

$$ \vec v = \vec n \times \vec u = \langle 4, -2, -2 \rangle $$

Note that if you take the dot product between any of these two vectors, you will get $0$. Next, we must normalize these vectors (divide them by their magnitude).

$$ \vec u = \langle 0, 1, -1 \rangle / \sqrt{2} $$ $$ \vec v = \langle 4, -2, -2 \rangle / \sqrt{24} $$

Next we will find the center of this circle. The center of the circle must lie on our plane, so we will find when the line that has a direction vector as the normal of the plane intersects the plane. This point of intersection is our center. Note that in our line, $p_0 = \langle 0, 0, 0 \rangle$.

$$ \vec l(t) = \vec n t = \langle -2, -2, -2 \rangle t = \langle -2t, -2t, -2t \rangle $$

If we plug in the components of this vector into our plane, we will find the $t$ value of the intersection.

$$ -2 (-2t) - 2(-2t) - 2(-2t) = -3 $$ $$ 4t + 4t + 4t = -3 $$ $$ t = -\frac{1}{4} $$

We will now substitute in $-\frac{1}{4}$ for $t$ in our line.

$$\vec c = \vec l \left(-\frac{1}{4} \right) = \left\langle \frac{1}{2}, \frac{1}{2}, \frac{1}{2} \right\rangle $$

Now we have everything except the radius. I admit, I am completely drawing a blank on how to find the radius. I've thought about it for a while, but I just have no idea. Experimental evidence (Grapher app on Macs) Mac OSX) has concluded that the radius is equal to $\frac{1}{2}$, but why? If someone could clarify, I would be so happy!

This is the circle with a radius of $0.5$:

As it stands, here is our equation:

$$ \vec p(t) = \left\langle \frac{1}{2}, \frac{1}{2}, \frac{1}{2} \right\rangle + r\cos(t)\frac{\langle 0, 1, -1 \rangle}{\sqrt{2}} + r\sin(t)\frac{\langle 4, -2, -2 \rangle}{\sqrt{24}} $$

So if anyone knows how to find the radius... please let me know!

I agree with Tiffany about everything except the radius and $\vec u$ and $\vec v$. Just for the sake of completion, I will go over all my steps.

The general equation for a parametrized circle is as follows:

$$ \vec p(t) = \vec c + r \cos(t) \vec u + r \sin(t) \vec v $$

The first piece of information that we must find is an equation describing the plane that the circle lies in. We do this by setting the equations of the spheres equal to each other. Since the radii are both equal to 1, we don't have to wrry about adding or subtracting constants.

$$ x^2 + y^2 + z^2 = (x-1)^2 + (y-1)^2 + (z-1)^2 $$ $$ x^2 + y^2 + z^2 = (x^2 - 2x + 1) + (y^2 - 2y + 1) + (z^2 - z + 1) $$

After rearranging the terms, we obtain:

$$ - 2x - 2y - 2z = -3 $$

This is the equation for our plane. This problem can now be thought of as the intersection of the unit sphere and this plane.

The next piece of information we need is the normal vector to the plane. This is easy!

$$ \vec n = \langle -2, -2, -2 \rangle $$

Now we can find $\vec u$ and $\vec v$. To find $\vec u$, I will choose a random vector that is perpendicular to $\vec n$ (i.e. one that lies on our plane).

$$ \vec u = \langle 0, 1, -1 \rangle $$

Note that $\vec n \cdot \vec u = 0$. We will now cross $\vec n$ with $\vec u$ to find a vector that is perpendicular to both of them.

$$ \vec v = \vec n \times \vec u = \langle 4, -2, -2 \rangle $$

Note that if you take the dot product between any of these two vectors, you will get $0$. Next, we must normalize these vectors (divide them by their magnitude).

$$ \vec u = \langle 0, 1, -1 \rangle / \sqrt{2} $$ $$ \vec v = \langle 4, -2, -2 \rangle / \sqrt{24} $$

Next we will find the center of this circle. The center of the circle must lie on our plane, so we will find when the line that has a direction vector as the normal of the plane intersects the plane. This point of intersection is our center. Note that in our line, $p_0 = \langle 0, 0, 0 \rangle$.

$$ \vec l(t) = \vec n t = \langle -2, -2, -2 \rangle t = \langle -2t, -2t, -2t \rangle $$

If we plug in the components of this vector into our plane, we will find the $t$ value of the intersection.

$$ -2 (-2t) - 2(-2t) - 2(-2t) = -3 $$ $$ 4t + 4t + 4t = -3 $$ $$ t = -\frac{1}{4} $$

We will now substitute in $-\frac{1}{4}$ for $t$ in our line.

$$\vec c = \vec l \left(-\frac{1}{4} \right) = \left\langle \frac{1}{2}, \frac{1}{2}, \frac{1}{2} \right\rangle $$

Now we have everything except the radius. I admit, I am completely drawing a blank on how to find the radius. I've thought about it for a while, but I just have no idea. Experimental evidence (Grapher on Mac OSX) has concluded that the radius is equal to $\frac{1}{2}$, but why? If someone could clarify, I would be so happy!

This is the circle with a radius of $0.5$:

As it stands, here is our equation:

$$ \vec p(t) = \left\langle \frac{1}{2}, \frac{1}{2}, \frac{1}{2} \right\rangle + r\cos(t)\frac{\langle 0, 1, -1 \rangle}{\sqrt{2}} + r\sin(t)\frac{\langle 4, -2, -2 \rangle}{\sqrt{24}} $$

So if anyone knows how to find the radius... please let me know!

I agree with Tiffany about everything except the radius and $\vec u$ and $\vec v$. Just for the sake of completion, I will go over all my steps.

The general equation for a parametrized circle is as follows:

$$ \vec p(t) = \vec c + r \cos(t) \vec u + r \sin(t) \vec v $$

The first piece of information that we must find is an equation describing the plane that the circle lies in. We do this by setting the equations of the spheres equal to each other. Since the radii are both equal to 1, we don't have to wrry about adding or subtracting constants.

$$ x^2 + y^2 + z^2 = (x-1)^2 + (y-1)^2 + (z-1)^2 $$ $$ x^2 + y^2 + z^2 = (x^2 - 2x + 1) + (y^2 - 2y + 1) + (z^2 - z + 1) $$

After rearranging the terms, we obtain:

$$ - 2x - 2y - 2z = -3 $$

This is the equation for our plane. This problem can now be thought of as the intersection of the unit sphere and this plane.

The next piece of information we need is the normal vector to the plane. This is easy!

$$ \vec n = \langle -2, -2, -2 \rangle $$

Now we can find $\vec u$ and $\vec v$. To find $\vec u$, I will choose a random vector that is perpendicular to $\vec n$ (i.e. one that lies on our plane).

$$ \vec u = \langle 0, 1, -1 \rangle $$

Note that $\vec n \cdot \vec u = 0$. We will now cross $\vec n$ with $\vec u$ to find a vector that is perpendicular to both of them.

$$ \vec v = \vec n \times \vec u = \langle 4, -2, -2 \rangle $$

Note that if you take the dot product between any of these two vectors, you will get $0$. Next, we must normalize these vectors (divide them by their magnitude).

$$ \vec u = \langle 0, 1, -1 \rangle / \sqrt{2} $$ $$ \vec v = \langle 4, -2, -2 \rangle / \sqrt{24} $$

Next we will find the center of this circle. The center of the circle must lie on our plane, so we will find when the line that has a direction vector as the normal of the plane intersects the plane. This point of intersection is our center. Note that in our line, $p_0 = \langle 0, 0, 0 \rangle$.

$$ \vec l(t) = \vec n t = \langle -2, -2, -2 \rangle t = \langle -2t, -2t, -2t \rangle $$

If we plug in the components of this vector into our plane, we will find the $t$ value of the intersection.

$$ -2 (-2t) - 2(-2t) - 2(-2t) = -3 $$ $$ 4t + 4t + 4t = -3 $$ $$ t = -\frac{1}{4} $$

We will now substitute in $-\frac{1}{4}$ for $t$ in our line.

$$\vec c = \vec l \left(-\frac{1}{4} \right) = \left\langle \frac{1}{2}, \frac{1}{2}, \frac{1}{2} \right\rangle $$

Now we have everything except the radius. I admit, I am completely drawing a blank on how to find the radius. I've thought about it for a while, but I just have no idea. Experimental evidence (Grapher on Mac OSX) has concluded that the radius is equal to $\frac{1}{2}$, but why? If someone could clarify, I would be so happy!

This is the circle with a radius of $0.5$:

As it stands, here is our equation:

$$ \vec p(t) = \left\langle \frac{1}{2}, \frac{1}{2}, \frac{1}{2} \right\rangle + r\cos(t)\frac{\langle 0, 1, -1 \rangle}{\sqrt{2}} + r\sin(t)\frac{\langle 4, -2, -2 \rangle}{\sqrt{24}} $$

So if anyone knows how to find the radius... please let me know!

Update

cbass, you are amazing on so many levels. I now see why the radius is $\frac{1}{2}$. This has been haunting me for hours haha! Thanks a ton!

I agree with Tiffany about everything except the radius and $\vec u$ and $\vec v$. Just for the sake of completion, I will go over all my steps.

The general equation for a parametrized circle is as follows:

$$ \vec p(t) = \vec c + r \cos(t) \vec u + r \sin(t) \vec v $$

The first piece of information that we must find is an equation describing the plane that the circle lies in. We do this by setting the equations of the spheres equal to each other. Since the radii are both equal to 1, we don't have to wrry about adding or subtracting constants.

$$ x^2 + y^2 + z^2 = (x-1)^2 + (y-1)^2 + (z-1)^2 $$ $$ x^2 + y^2 + z^2 = (x^2 - 2x + 1) + (y^2 - 2y + 1) + (z^2 - z + 1) $$

After rearranging the terms, we obtain:

$$ - 2x - 2y - 2z = -3 $$

This is the equation for our plane. This problem can now be thought of as the intersection of the unit sphere and this plane.

The next piece of information we need is the normal vector to the plane. This is easy!

$$ \vec n = \langle -2, -2, -2 \rangle $$

Now we can find $\vec u$ and $\vec v$. To find $\vec u$, I will choose a random vector that is perpendicular to $\vec n$ (i.e. one that lies on our plane).

$$ \vec u = \langle 0, 1, -1 \rangle $$

Note that $\vec n \cdot \vec u = 0$. We will now cross $\vec n$ with $\vec u$ to find a vector that is perpendicular to both of them.

$$ \vec v = \vec n \times \vec u = \langle 4, -2, -2 \rangle $$

Note that if you take the dot product between any of these two vectors, you will get $0$. Next, we must normalize these vectors (divide them by their magnitude).

$$ \vec u = \langle 0, 1, -1 \rangle / \sqrt{2} $$ $$ \vec v = \langle 4, -2, -2 \rangle / \sqrt{24} $$

Next we will find the center of this circle. The center of the circle must lie on our plane, so we will find when the line that has a direction vector as the normal of the plane intersects the plane. This point of intersection is our center. Note that in our line, $p_0 = \langle 0, 0, 0 \rangle$.

$$ \vec l(t) = \vec n t = \langle -2, -2, -2 \rangle t = \langle -2t, -2t, -2t \rangle $$

If we plug in the components of this vector into our plane, we will find the $t$ value of the intersection.

$$ -2 (-2t) - 2(-2t) - 2(-2t) = -3 $$ $$ 4t + 4t + 4t = -3 $$ $$ t = -\frac{1}{4} $$

We will now substitute in $-\frac{1}{4}$ for $t$ in our line.

$$\vec c = \vec l \left(-\frac{1}{4} \right) = \left\langle \frac{1}{2}, \frac{1}{2}, \frac{1}{2} \right\rangle $$

Now we have everything except the radius. I admit, I am completely drawing a blank on how to find the radius. I've thought about it for a while, but I just have no idea. Experimental evidence (Grapher on Mac OSX) OS X) has concluded that the radius is equal to $\frac{1}{2}$, but why? If someone could clarify, I would be so happy!

This is the circle with a radius of $0.5$:

As it stands, here is our equation:

$$ \vec p(t) = \left\langle \frac{1}{2}, \frac{1}{2}, \frac{1}{2} \right\rangle + r\cos(t)\frac{\langle 0, 1, -1 \rangle}{\sqrt{2}} + r\sin(t)\frac{\langle 4, -2, -2 \rangle}{\sqrt{24}} $$

So if anyone knows how to find the radius... please let me know!

Update

cbass, you are amazing on so many levels. I now see why the radius is $\frac{1}{2}$. This has been haunting me for hours haha! Thanks a ton!