-
A radial heat flow problem
(1) We start by separating variables, and assume $u(r,t) = R(r)T(t)$. Our PDE then becomes
$$(RT)_t = (RT)_{rr} + \frac{1}{r}(RT)_r$$ or
$$RT' = R''T + \frac{1}{r}R'T.$$
Dividing both sides by $RT$, we get
$$\frac{T'}{T} = \frac{R''}{R} +\frac{1}{r}\frac{R'}{R} = -\lambda.$$
Thus, $\frac{T'}{T} = -\lambda$, so $T' = -\lambda T.$ Hence,
$$T = e^{-\lambda t}.$$ Meanwhile,
$$\frac{R''}{R} + \frac{1}{r}\frac{R'}{R} = -\lambda,$$ so
$$R'' + \frac{1}{r}R' = -\lambda R.$$
This can be rewritten as $$-(rR'(r))' = \lambda rR(r).$$
The solutions to this radial differential equation are the Bessel functions $$R(r) = c_1J_0\left(\sqrt{\lambda}r\right) + c_2Y_0\left(\sqrt{\lambda}r\right).$$
Since $Y_0$ is unbounded at $z=0, c_2$ must equal $0,$ so $$R(r) = c_1J_0\left(\sqrt{\lambda}r\right).$$
From our boundary conditions, we know $$R(1) = c_1J_0\left(\sqrt{\lambda}\right) = 0,$$ so
$$\sqrt{\lambda} = z_n, n=1,2,3...$$
where $z_n$ are the zeros of $J_0.$ Hence, the eigenvalues are $\lambda_n = z_n^2$ and the corresponding eigenfunctions are $R_n(r) = J_0(z_nr).$ Thus, our full solution is
$$u(r,t) = \sum_{n=1}^{\infty}c_ne^{-\lambda_n^2t}J_0(z_nr).$$
(2) By our initial conditions,
$$u(r,0) = \sum_{n=1}^{\infty}c_nJ_0(z_nr) = 5r^3(1-r).$$
Since Bessel functions satisfy the orthogonality condition,
$$c_n = \frac{\int_{0}^{1}5r^3(1-r)J_0(z_nr)rdr}{\int_{0}^{1}J_0^2(z_nr)^2rdr}.$$
Plugging an initial condition $u(r,0)$ into the "Radial heat flow" ObservableHQ page gives us the normalized Bessel function $F(r)$ for each term of the solution and its constant coefficient, which we'll denote $b_n,$ where
$$u(r,0) = \sum_{n=1}^{\infty}b_nF_n(r) = \sum_{n=1}^{\infty}b_n\frac{R_n(r)}{||R_n||}.$$
Since $u(r,0) = \sum_{n=1}^{\infty}c_nR_n(r),$ it follows that
$$c_n = \frac{b_n}{||R_n||}.$$
We plug in $u(r,0) = 5r^3(1-r)$ and find that
$$u(r,t) \approx \frac{0.17333401324973097}{0.3670927157694067}e^{-z_1^2t}J_0(z_1r) + \frac{-0.18156860394077448}{0.24060355211655088}e^{-z_2^2t}J_0(z_2r) + \frac{0.0731801393963544}{0.16437392311147672}e^{-z_3^2t}J_0(z_3r)$$
$$= 0.4721804759e^{-z_1^2t}J_0(z_1r) - 0.7546380855e^{-z_2^2t}J_0(z_2r) + 0.4452052857e^{-z_3^2t}J_0(z_3r)$$
(3)
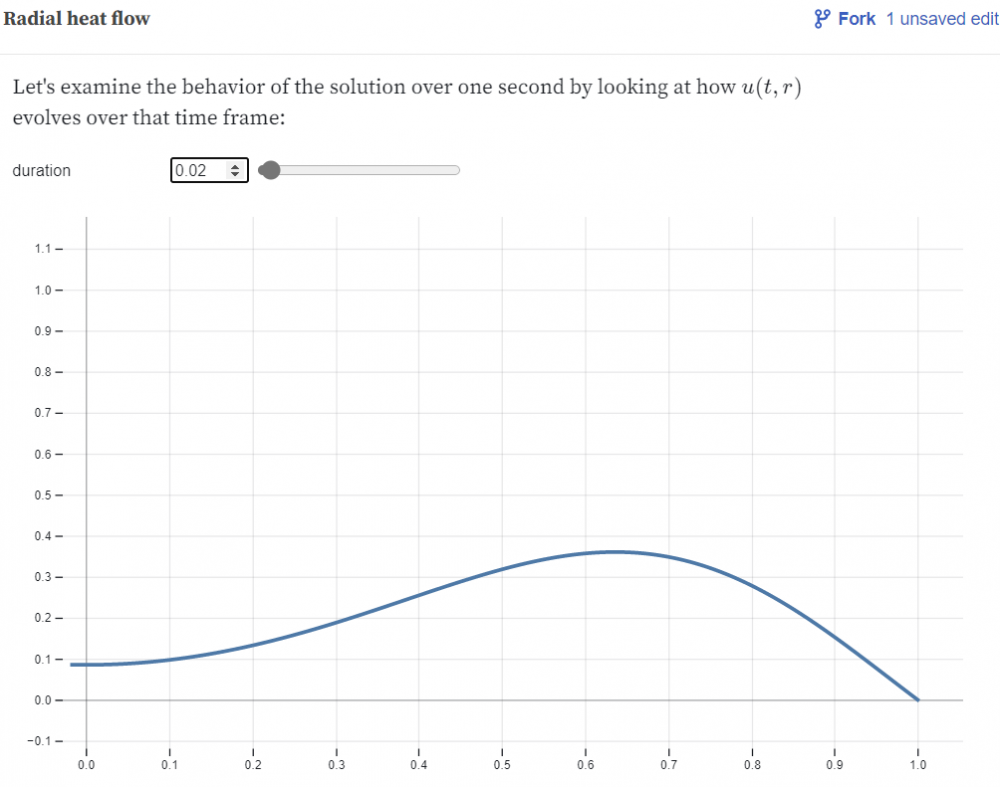
Using the same Observable page, with N=10, we graph the function at time $t = 0.02$:
(4)
Using the final tool on the Observable page with $N=10$, we find $$u(0, 0.02) = 0.086.$$
-
Eigenranking
My matrix was:
matrix = [
[0,1,4,3,3],
[2,0,2,4,3],
[3,3,0,3,2],
[2,1,1,0,2],
[3,1,3,1,0]
]
and my ranking was:
Team 3: rating = 0.5054388063612655 Team 1: rating = 0.5016207712530641 Team 2: rating = 0.48157957363128245 Team 5: rating = 0.4108981576640922 Team 4: rating = 0.30356553355238997
Team 3 was the best.
-
Modeling a steady state heat distribution in 2D
-
Modeling 2D Heat Flow
-
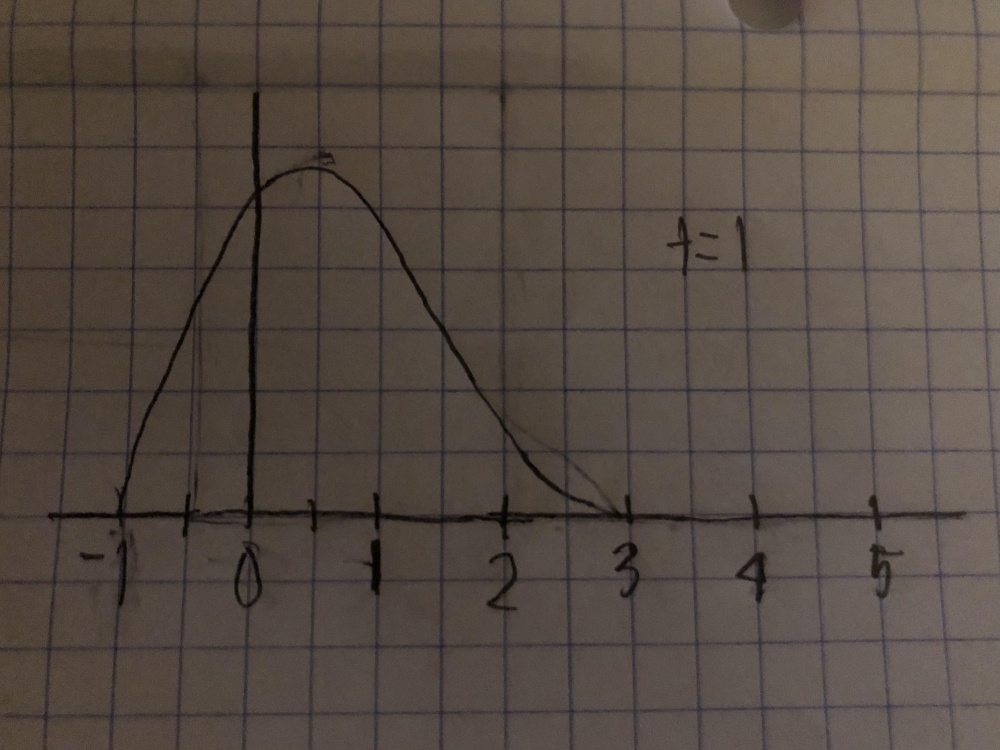
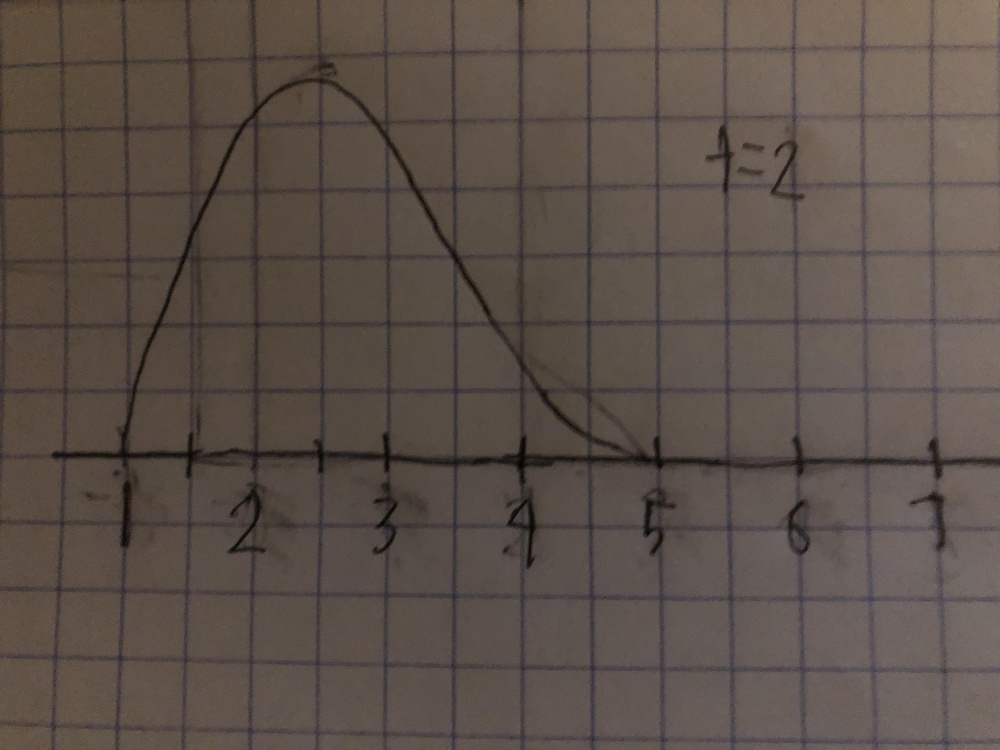
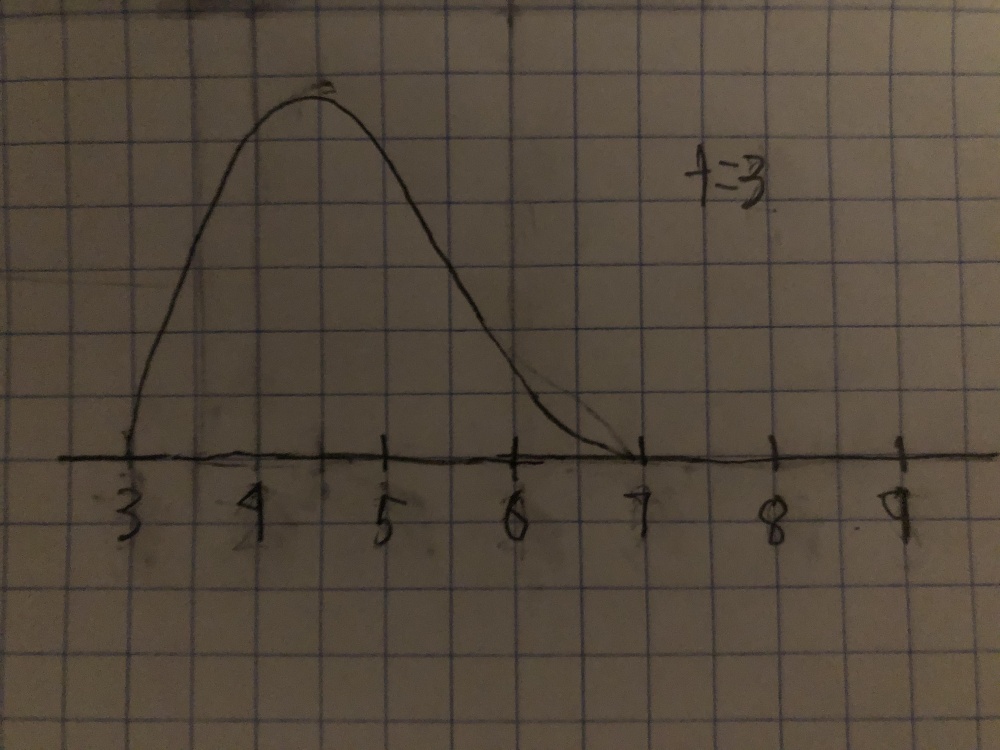
First order sketches
The solution to the PDE is
$$u = u_0(x - 2t),$$
so at each time interval, the graph above will shift to the right by two units. Here are sketches of the graph at each of the three times:
If we changed the PDE to $u_t + 2u_x = -u$, the solution becomes
$$u = u_0(x - 2t)e^{-t},$$
so $u$ will decay over time, approaching zero at large values of $t$.