-
Eigenranking
My matrix was
matrix = [
[0, 4, 4, 4, 2],
[2, 0, 3, 4, 4],
[3, 1, 0, 3, 3],
[2, 1, 1, 0, 1],
[2, 3, 2, 2, 0]
]
The eigenranking was
Team 1: rating = 0.5676428888501164 Team 2: rating = 0.5140250259852949 Team 3: rating = 0.4266803335123048 Team 5: rating = 0.4096681506358447 Team 4: rating = 0.25234048971012685
And team 1 was the best.
-
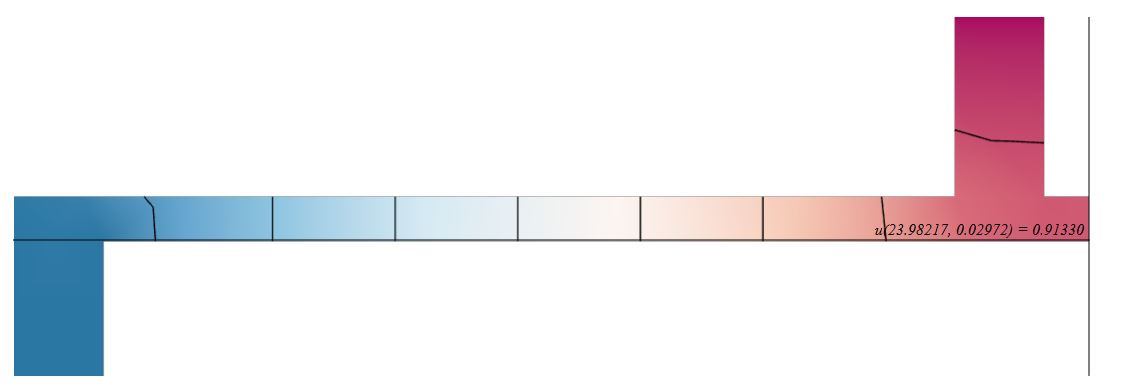
Modeling a steady state heat distribution in 2D
-
Steady state heat flow with source
The equation for heat flow in my problem is
$$u_t=4u_{xx}+3$$
with boundary conditions $u(0,t)=-3$ and $u(1,t)=2$.
To find the steady state solution, we set $u_t=0$. Then,
$$0=4u_{xx}+3$$
$$\Rightarrow u_{xx}=-\frac{4}{3}$$
$$\Rightarrow u_{x}=-\frac{4}{3}x+\alpha$$
$$\Rightarrow u(x)=-\frac{2}{3}x^2+\alpha x+\beta.$$
Inserting the boundary conditions, we get
$$u(0)=\beta=-3$$
and
$$u(1)=-\frac{2}{3}+\alpha-3=2$$
$$\Rightarrow \alpha=\frac{17}{3}.$$
Therefore, the steady state solution is
$$\boxed{u(x,t)=-\frac{2}{3}x^2+\frac{17}{3}x-3}$$
-
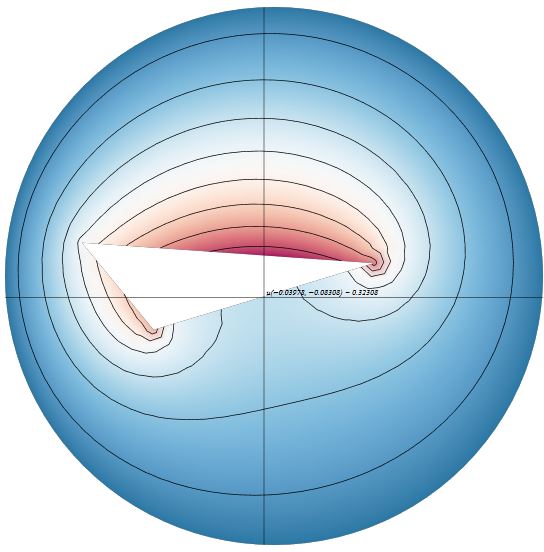
Modeling 2D Heat Flow
-
A vector identity
$\textbf{Theorem}$. Suppose $\omega(x,y,z)$ is a scalar field and $\vec{\varphi}(x,y,z)$ is a vector field. Then,
$$\nabla\cdot\left(\omega\vec{\varphi}\right)=\vec{\varphi}\cdot\nabla\omega+\omega\nabla\cdot\vec{\varphi}.$$
$\textit{Proof.}$
$$\nabla\cdot\left(\omega\vec{\varphi}\right)=\left\langle \frac{\partial}{\partial x},\frac{\partial}{\partial y}, \frac{\partial}{\partial z}\right\rangle\cdot\omega\left\langle\varphi_x,\varphi_y,\varphi_z\right\rangle$$
$$=\left\langle \frac{\partial}{\partial x},\frac{\partial}{\partial y}, \frac{\partial}{\partial z}\right\rangle\cdot\left\langle\omega\varphi_x,\omega\varphi_y,\omega\varphi_z\right\rangle$$
$$=\frac{\partial(\omega\varphi_x)}{\partial x}+\frac{\partial(\omega\varphi_y)}{\partial y}+\frac{\partial(\omega\varphi_z)}{\partial z}$$
$$=\left(\frac{\partial\omega}{\partial x}\varphi_x+\frac{\partial\varphi_x}{\partial x}\omega\right)+\left(\frac{\partial\omega}{\partial y}\varphi_y+\frac{\partial\varphi_y}{\partial y}\omega\right)+\left(\frac{\partial\omega}{\partial z}\varphi_z+\frac{\partial\varphi_z}{\partial z}\omega\right)$$
$$=\left(\varphi_x\frac{\partial\omega}{\partial x}+\varphi_y\frac{\partial\omega}{\partial y}+\varphi_z\frac{\partial\omega}{\partial z}\right)+\omega\left(\frac{\partial\varphi_x}{\partial x}+\frac{\partial\varphi_y}{\partial y}+\frac{\partial\varphi_z}{\partial z}\right)$$
$$=\vec{\varphi}\cdot\nabla\omega+\omega\nabla\cdot\vec{\varphi}. $$
$$ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \square$$