-
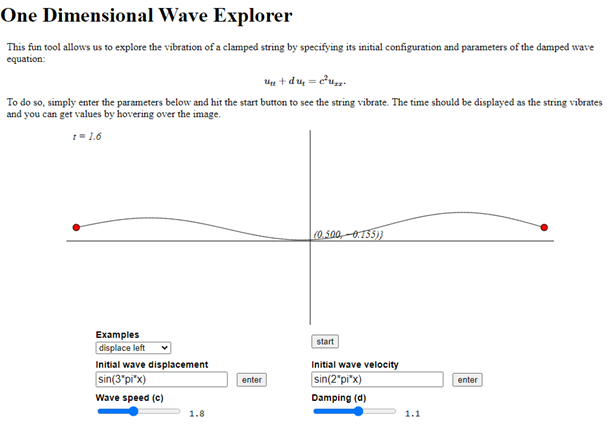
A random vibration problem
-
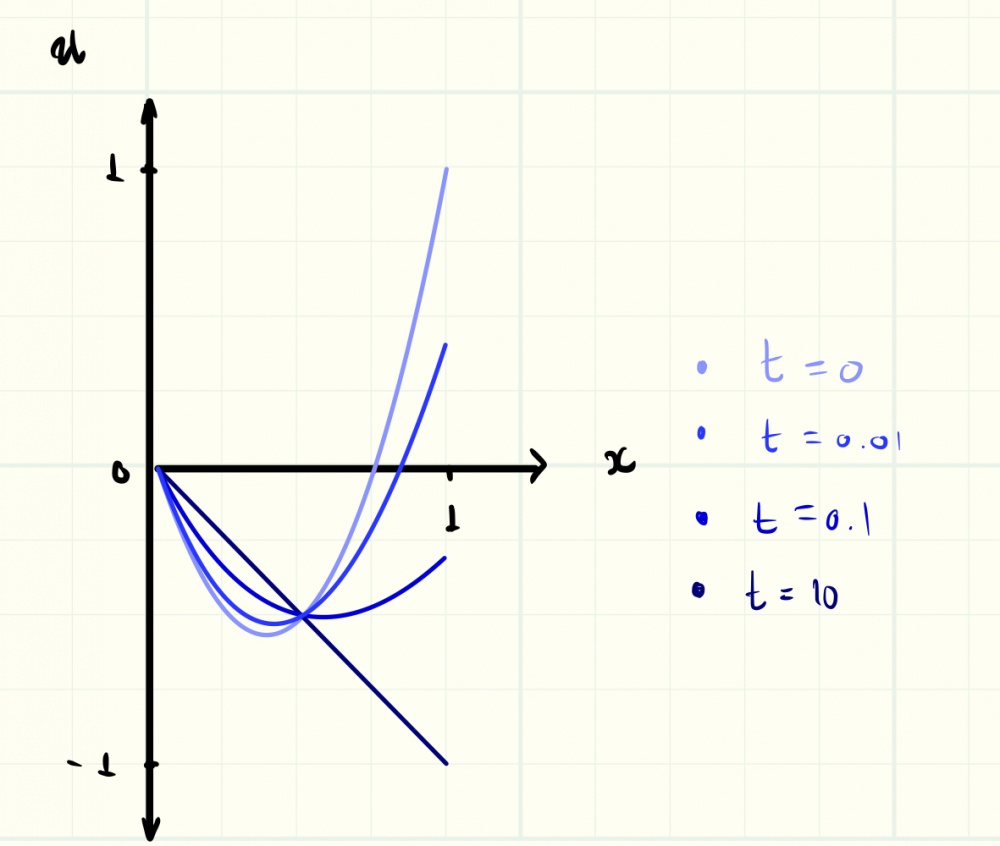
Random heat evolution problem
-
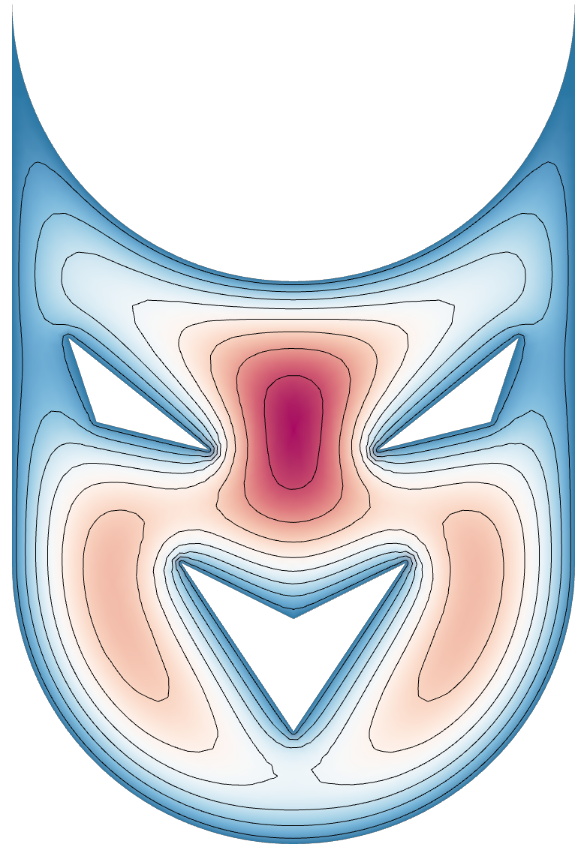
Smile
-
Eigenranking
-
Approximating an eigenfunction
I tried the following:
a = 0
b = 2
n =25
1) The 24x24 matrix that approximates the 2nd derivative is
$$U_{xx}=\begin{pmatrix} -312.5 & 156.25 & 0 & \ldots & 0 & 0 & 0\\ 156.25 & -312.5 & 156.25 & \ldots & 0 & 0 & 0\\ \ldots & \ldots & \ldots & \ldots & \ldots & \ldots & \ldots\\ 0 & 0 & 0 &\ldots & 156.25 & -312.5 & 156.25\\ 0 & 0 & 0 & \ldots & 0 & 156.25 & -312.5 \end{pmatrix}$$
2) The eigenvalue of smallest magnitude and its corresponding eigenvector are:
$$\lambda = -2.4642$$
$$\vec u = \begin{pmatrix} -0.0354\\ -0.0703\\-0.1041\\-0.1362\\-0.1662\\-0.1936\\-0.2179\\-0.2388\\-0.2559\\-0.2689\\-0.2778\\-0.2822\\-0.2822\\-0.2778\\-0.2689\\-0.2559\\-0.2388\\-0.2179\\-0.1936\\-0.1662\\-0.1362\\-0.1041\\-0.0703\\-0.0354\end{pmatrix}$$
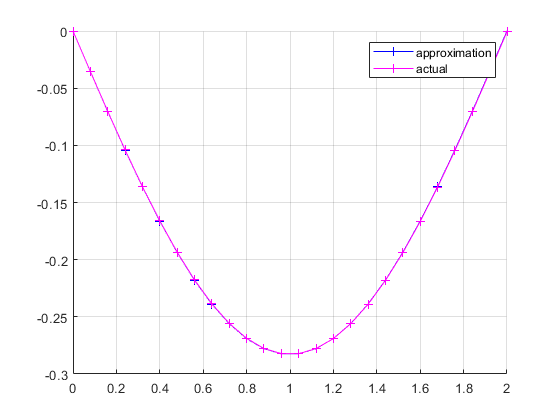
3) The eigenfunction for this problem was: $$k* sin(\sqrt{-\lambda}*x)$$.
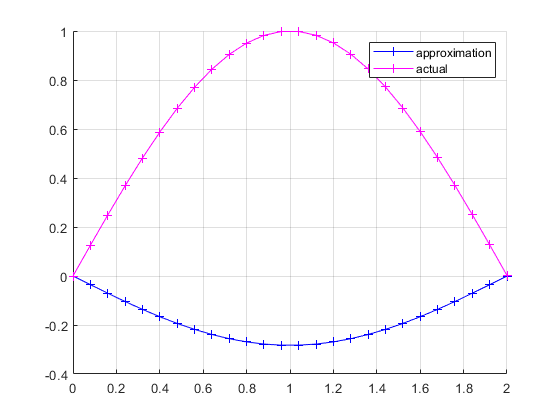
If we drop k, we get the following plot:
But if we let $k = -0.09\pi$, we get the following:
Now, I don't remember talking about using the approximation to find $k$ in class. @mark Could you explain why this was necessary here?
-
Modeling 2D Heat Flow
-
Modeling a steady state heat distribution in 2D
-
Steady state heat flow with source
Heat flow with a constant internal heat source is governed by the following model:
$$u_t = 4u_{xx} + 5$$
Find the steady-state temperature distribution $u(x,t)$ if the boundary conditions are:
$$u( 0, t) = -2; u( 1, t) = 4$$
Steady-state implies that nothing changes with time, therefore:
$$\frac{du}{dt} = 0$$
Plugging the result into the model and rearranging the terms:
$$u_{xx} = - \frac{5}{4}$$
Integrate twice:
$$u_x = - \frac{5}{4} x + \phi (t)$$
$$u = - \frac{5}{8} x^2 + \phi (t)x + \psi (t)$$
Use boundary conditions to determine the unknown functions $\phi (t)$ and $\psi (t)$
$$u(0, t) = \psi (t) = -2$$
$$u(1, t) = -\frac{5}{8} + \phi (t) + (-2) = 4 \rightarrow \phi(t) = \frac{53}{8}$$
Therefore, the steady state temperature distribution is:
$$\boxed{u(x,t) = - 0.625 x^2 + 9.6 x -2}$$