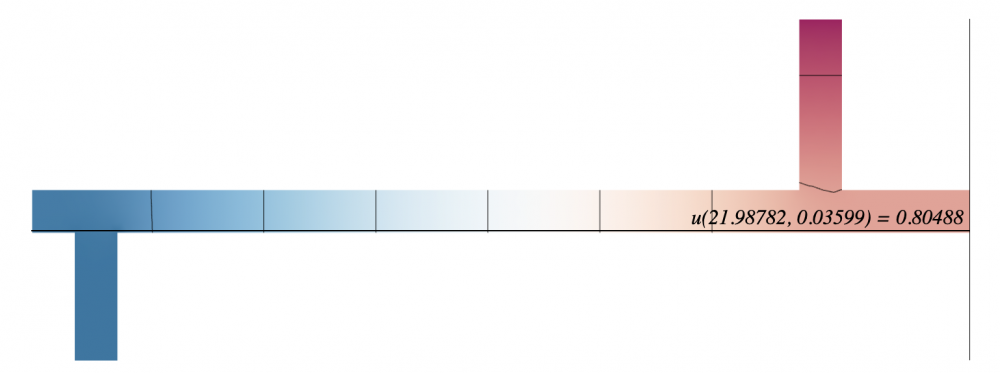-
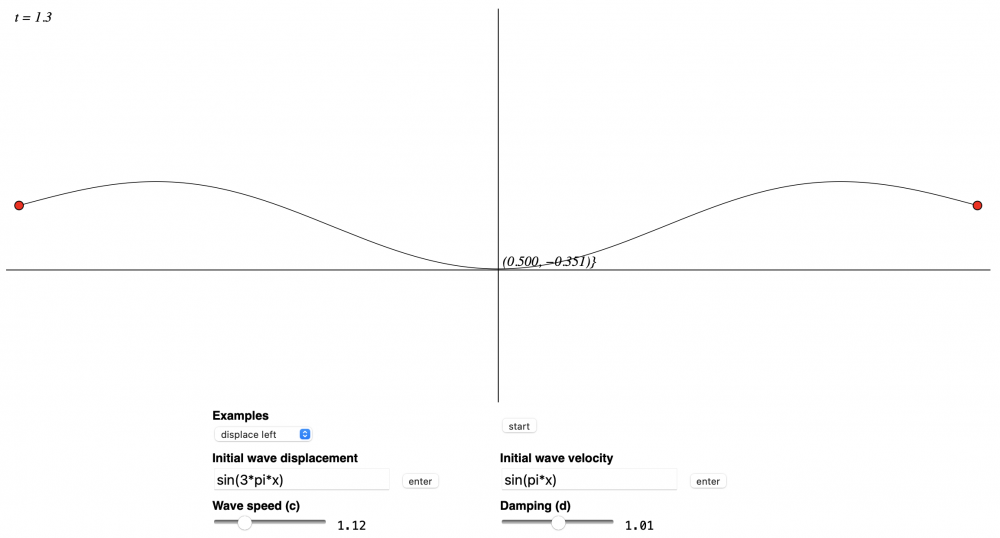
A random vibration problem
-
Steady state heat flow with source
Heat flow with a constant internal heat source is governed by:
$$u_t = 1u_{xx} + 2, u(0,t) = -3, u(1,t) = 5.$$
When at the steady state temperature distribution, $u_t = 0$ therefore:
$$0 = u_{xx} + 2$$
This can be rearranged to give $u_{xx} = -2$. Next this function was integrated with respect to $x$ twice giving $$u(x) = -1x^2 + \alpha*x + \beta$$.
Plugging in the conditions $u(0,t) = -3$ and $u(1,t) = 5$ allowed for finding of $\alpha = 9$ and $\beta = -3$.
Therefore, the steady state temperature distribution is:
$$u(x) = -1x^2 + 9x - 3$$
-
Random heat evolution problem
-
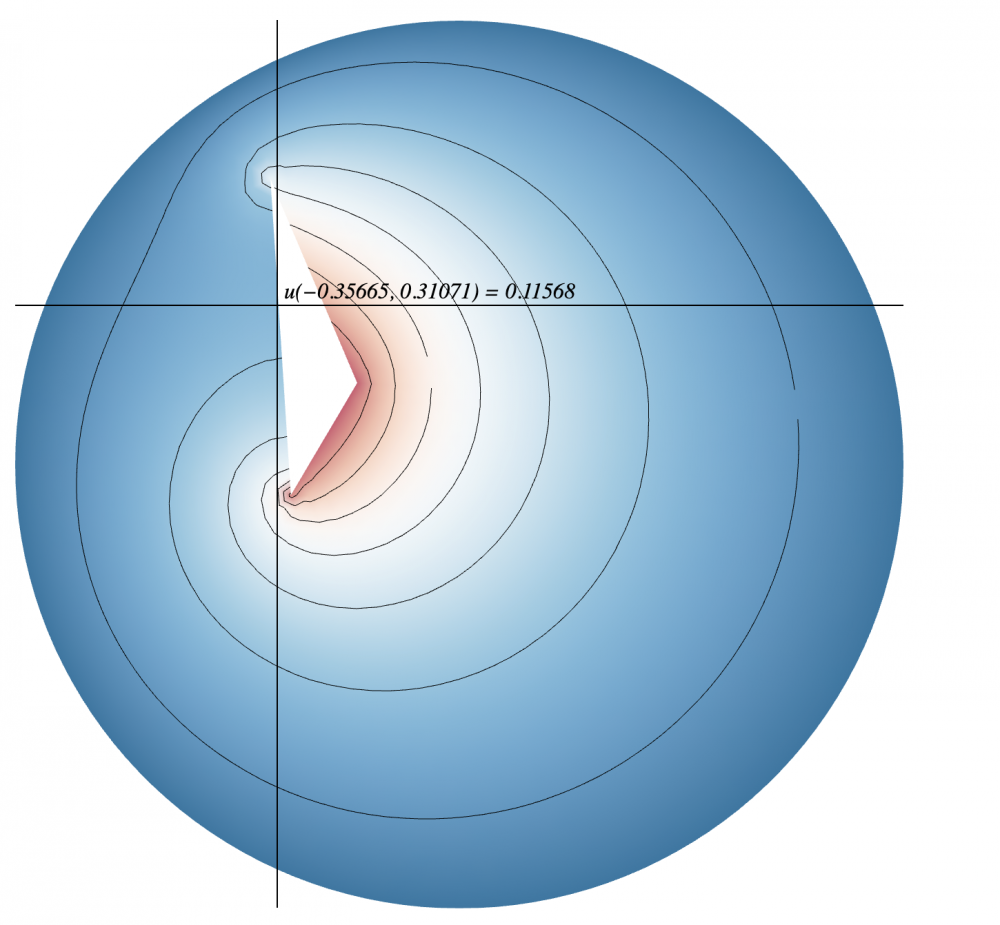
Modeling 2D Heat Flow
For my problem, the basic heat equation was:
$$u_t = 0.47\Delta u$$
The vertical side of the triangle is insulated
The Dirichlet condition on the circle and the 2 other sides of the triangle is
$$u(x,y,t) = 0.87^2 - (x^2+y^2)$$
The initial condition is:
$$u(x,y,0) = 0.87^2 - (x^2+y^2)$$
I found the temperature of the domain near the midpoint of the insulated edge at time, $t = 0.99$s to be 0.11568
-
House
-
Full Fourier series
The full Fourier Series is generally:
$$f(x) \sim \frac{a_0}{2} + \sum_{n=1}^{\infty} a_ncos(\frac{n\pi x}{L}) + b_nsin(\frac{n\pi x}{L})$$
First find the value of $a_0$ for $f(x) = x - x^2$ over the interval $[0,L]$
$$a_0 = \frac{2}{L} \int_{0}^{L} f(x)\,dx$$
$$\implies a_0 = 4 \int_{0}^{\frac{1}{2}}(x - x^2)\,dx = 4\int_{0}^{\frac{1}{2}} x\,dx - \int_{0}^{\frac{1}{2}} x^2\,dx$$
$$\implies 4[\frac{1}{2} x^2 \biggr\rvert_{0}^{\frac{1}{2}} - \frac{1}{3} x^3 \biggr\rvert_{0}^{\frac{1}{2}}] = 4[\frac{1}{2} (\frac{1}{2})^2 - \frac{1}{3} (\frac{1}{2})^3]$$
$$\implies 4[\frac{1}{8} - \frac{1}{24}] = 4(\frac{1}{12})$$
Therefore $a_0 = \frac{1}{3}$ and plugging in this value into the general equation gives $\frac{a_0}{2} = \frac{1}{6}$
Next, find the value for $a_n$ for $f(x)$
$$\int_{0}^{L} f(x)cos(\frac{n\pi x}{L})\,dx = 4\int_{0}^{\frac{1}{2}} (x - x^2)cos(2\pi nx)\,dx$$
Can split into integrals of $x$ and $x^2$
$$4\int_{0}^{\frac{1}{2}}xcos(2\pi nx)\,dx$$
Using integration by parts, with
$u = x, du = dx, v = \frac{sin(2\pi nx)}{2\pi n}, dv = cos(2\pi nx)dx$
$$\implies 4[ \frac{xsin(2\pi nx)}{2\pi n} \bigg\rvert_{0}^{\frac{1}{2}} - \frac{1}{2\pi n} \int_{0}^{\frac{1}{2}}sin(2\pi nx)\,dx ]$$
$$\implies \frac{1}{(\pi n)^2} cos(2\pi nx) \bigg\rvert_{0}^{\frac{1}{2}} = \frac{1}{(\pi n)^2} [(-1)^n - 1] = \frac{(-1)^n -1}{\pi^2n^2}$$
Now, plugging in $x^2$ gives
$$4 \int_{0}^{\frac{1}{2}} x^2cos(2\pi nx)\,dx$$
Again using integration by parts, with
$u = x^2, du = 2xdx, v = \frac{sin(2\pi nx)}{2\pi n}, dv = cos(2\pi nx)dx$
$$\implies 4[ \frac{(x^2)sin(2\pi nx)}{2\pi n} \bigg\rvert_{0}^{\frac{1}{2}} - \frac{1}{\pi n} \int_{0}^{\frac{1}{2}} xsin(2\pi nx)\,dx ]$$
The first term is equal to $0$, and integration by parts must be used to solve the integral with
$u = x, du = dx, v = \frac{-cos(2\pi nx)}{2\pi n}, dv = sin(2\pi nx)dx$
$$\implies \frac{-4}{\pi n} \frac{-xcos(2\pi nx)}{2\pi n} \bigg\rvert_{0}^{\frac{1}{2}} + \frac{1}{2\pi n} \int_{0}^{\frac{1}{2}} cos(2\pi nx)\,dx$$
$$\implies \frac{4}{\pi n}(\frac{(-1)^n}{4\pi n}) = \frac{(-1)^n}{\pi^2n^2}$$
$$\implies a_n = \frac{(-1)^n - 1}{\pi^2n^2} - \frac{(-1)^n}{\pi^2n^2} = \frac{(-1)}{\pi^2n^2}$$
Now move onto $b_n$ and again split the integrals of $x$ and $x^2$
$$b_n = \frac{2}{L} \int_{0}^{L} f(x)sin(\frac{\pi nx}{L})\,dx $$
$$b_n = 4[\int_{0}^{\frac{1}{2}} xsin(2\pi nx)\,dx - \int_{0}^{\frac{1}{2}} x^2sin(2\pi nx)\,dx ]$$
Use integration by parts for the integral of $x$, with
$u = x, du = dx, v = \frac{-cos(2\pi nx)}{2\pi n}, dv = sin(2\pi nx)dx$
$$\implies 4[\frac{-xcos(2\pi nx)}{2\pi n} \bigg\rvert_{0}^{\frac{1}{2}} + \frac{1}{2\pi n} \int_{0}^{\frac{1}{2}} cos(2\pi nx)\,dx ]$$
$$\implies 4[-\frac{(-1)^n}{4\pi n}] = -\frac{(-1)^n}{\pi n}$$
Use integration by parts for the integral of $x^2$, with
$u = x^2, du = 2xdx, v = \frac{-cos(2\pi nx)}{2\pi n}, dv = sin(2\pi nx)dx$
$$\implies 4[\frac{-x^2cos(2\pi nx)}{2\pi n} \bigg\rvert_{0}^{\frac{1}{2}} + \frac{1}{\pi n} \int_{0}^{\frac{1}{2}} xcos(2\pi nx)\,dx ]$$
$$\implies 4[-\frac{(-1)^n}{8\pi n}] = -\frac{(-1)^n}{2\pi n}$$
$$\implies b_n = -\frac{(-1)^n}{\pi n} + \frac{(-1)^n}{2\pi n} = -\frac{(-1)^n}{2\pi n}$$
Therefore, the full Fourier Series for $f(x) = x - x^2$ over $[0,\frac{1}{2}]$ is:
$$\frac{1}{6} + \sum_{n=1}^{\infty} \frac{(-1)}{\pi^2n^2}cos(2\pi nx) - \frac{(-1)^n}{2\pi n}sin(2\pi nx)$$
This differs from the Fourier series we saw in class as it contains both the Fourier Sine series and the Fourier Cosine series.
-
Eigenranking
-
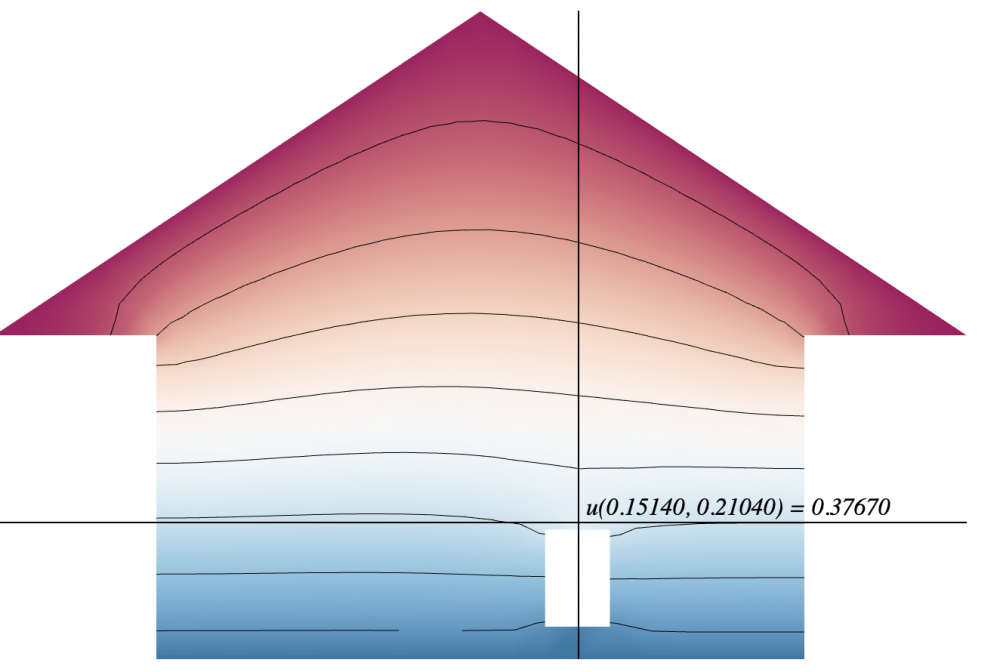
Modeling a steady state heat distribution in 2D
For my unique conditions, $\kappa = 0$ and $f = 0$. The three sides on the lower left, sticking out of the bar, are set to temperature zero. The side at the very top of the rectangle on the upper right is set to temperature 1. The remaining sides are insulated. At the steady state for the heat distribution, the temperature for the lower right corner of the bar is $u = 0.80488$.