• Home

    • Best Awesome Content

    • Exam Question

      mega_late mega_late

      Check it 1,2,
      recall that azimuthal projection satisfy the equation $T(\phi,\theta)=(r(\phi)cos(\theta),r(\phi)sin(\theta))$. Then $T_{\phi}=((r'(\phi)cos(\theta),r'(\phi)sin(\theta))$ and $T_{\theta}=((r(\phi)(-sin(\theta)),r(\phi)cos(\theta))$. Then $T_{\phi} \cdot T_{\theta} = ((r'(\phi)cos(\theta),r'(\phi)sin(\theta)) \cdot ((r(\phi)(-sin(\theta)),r(\phi)cos(\theta)) = (r'(\phi)cos(\theta))(r(\phi)(-sin(\theta))) + (r'(\phi)sin(\theta))(r(\phi)cos(\theta)) = -(r'(\phi)cos(\theta))(r(\phi)(sin(\theta))) + (r'(\phi)sin(\theta))(r(\phi)cos(\theta)) = 0$

      mark

    • Another Exam Question

      mega_late mega_late

      Prove that every cylindrical map projection satisfies $T_{\phi} \cdot T_{\theta}=0$

      mark

    • Exam Question

      lusta lusta

      I was very curious about number 7,

      Prove the every polar azimuthal projection satisfies

      $T_\phi \cdot T_\theta = 0$.

      How can we show for $\textbf{every}$ azimuthal projection

      mark

    • Sahil wants points

      SighHillDoveN SighHillDoveN

      Using the code: 

      heatSystem = {
   D[u[x, t], t] == D[u[x, t], x, x],
   u[x, 0] == Sin[5 x],
   u[0, t] == 0, u[1, t] == 1};
u[x_, t_] = NDSolveValue[heatSystem,
  u[x, t], {x, 0, 1}, {t, 0, 1}]
Manipulate[Plot[u[x, t], {x, 0, 1},
  ColorFunction -> "TemperatureMap", 
  ColorFunctionScaling -> False,
  PlotRange -> {-1, 1}],
 {t, 0, 0.15}]
pics = Table[Plot[u[x, t], {x, 0, 1},
    ColorFunction -> "TemperatureMap", 
    ColorFunctionScaling -> False,
    PlotRange -> {-1, 1}],
   {t, 0, 0.5, 0.01}];
Export["anim.gif", pics]
u[0.5, 1]

      The graph of the solution is:

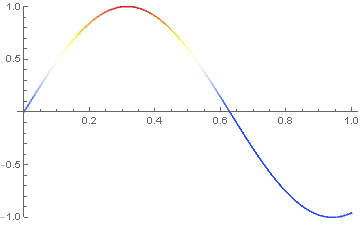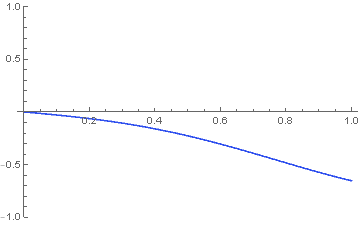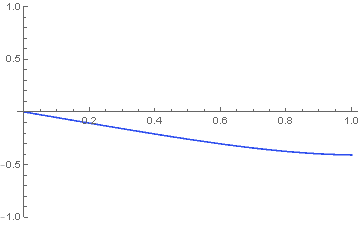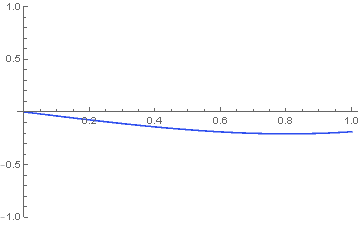
      The solution to the system $u_{t}=u_{xx}, u(x,0)=sin(5x), u(0,t)=0, u(1,t)=1$ at the midpoint when t=1 is:

      $u(0.5,1)=0.0894617$

      mark

    • Laplace's Equation and Steady State

      NegativeOneTwelfth NegativeOneTwelfth

      The equation is as follows.

      $$u=2x-1$$

      Notice that $u(0)=-1$, $u(2)=3$, and $\nabla^2u=0$.
      The graph is quite simple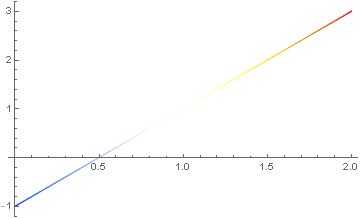

      If we think of the object as a bar, the $u$ value on the graph show the temperature of the bar at every point on the bar. This is a steady state heat flow equation because the temperature will not change with time.

      mark

    • Your favorite 3D function

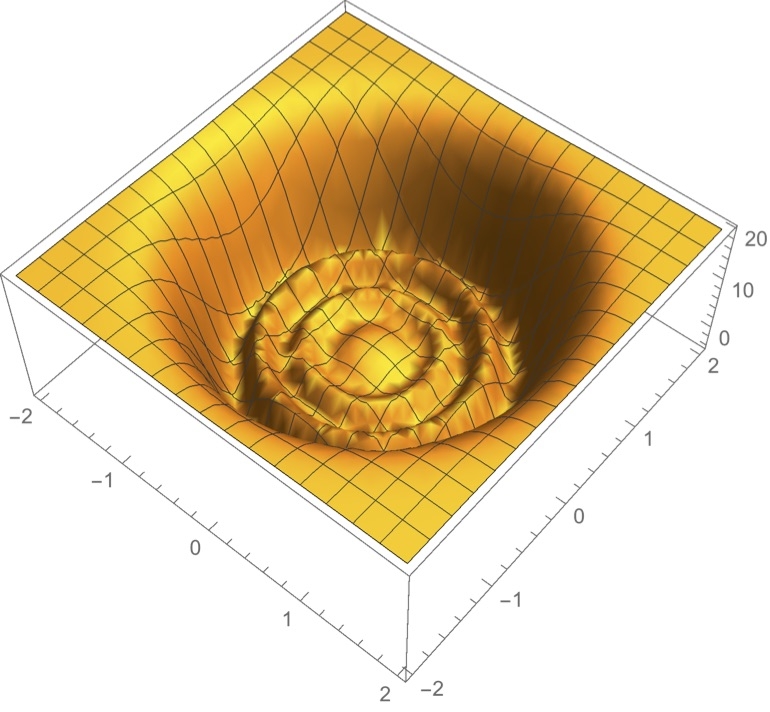
      super_duper_late_dude super_duper_late_dude


      Heres my favorite 3D function written in Cartesian coordinates $$F(x,y) = e^{x^2+y^2}sin(20e^{-x^2-y^2})$$

      It can also be represented in Polar coordinates as $$F(r,\theta) = e^{r^2}sin(20e^{-r^2})$$

      If you plot it in Mathematica Plot3D[E^(x^2 + y^2) Sin[20 E^(-x^2 - y^2)], {x, -2, 2}, {y, -2, 2}] it looks something like this

      mark

    • GreenDivergence Handout Problem 1

      Red Red

      For $\int_C F\cdot d n$ we have $\int_C F\cdot d n=\int \int \frac{\partial P}{\partial x}+\frac{\partial Q}{\partial y} dx dy$ and $\frac{\partial P}{\partial x}=2 $, $\frac{\partial Q}{\partial y}=1$. Thus, when converting to polar we have $\int_{0}^{2\pi} \int_{0}^1 3 r \text{ } dr d\theta=\int_0^{2\pi} \frac{3}{2} \space d\theta=3\pi$

      mark

    • Green's Theorem #3

      SighHillDoveN SighHillDoveN

      Suppose that $\text{div}\overrightarrow{F} = 2x + 3y$. Find the approximate flux of a vector field across a circle of
      radius 0.1 centered at the point (1, 1).

      mark

    • GreenDivergence Handout Problem 1

      SighHillDoveN SighHillDoveN

      For the integral $\int\limits_{C} F\cdot dr$,

      $\int\limits_{C} F\cdot dr=\int\limits_{0}^{2\pi}\int\limits_{0}^{1}r \bigg(\frac{\delta Q}{\delta x} - \frac{\delta P}{\delta y}\bigg)dx dy$

      $=\int\limits_{0}^{2\pi}\int\limits_{0}^{1}\bigg((-1)-(3)\bigg)dr d\theta$

      $=\int\limits_{0}^{2\pi}\int\limits_{0}^{1} r \bigg(-4\bigg)dr d\theta=-4\pi$

      mark

    • Greens Theorem Handout #2

      lusta lusta

      The first integral we can translate using Greens Theorem to be the integral over the rectangle $$\int_C F\cdot dr = \int_0^1 \int_0^1 Q_x - P_y dA$$
      After solving for the partial derivatives $Q_x$ and $P_y$ we find $$\int_0^1 \int_0^1 Q_x - P_y dA = \int_0^1 \int_0^1 -y-x dxdy = -1$$

      Now we can solve the second integral using greens theorem $$\int_C F\cdot dn = \int_0^1 \int_0^1 P_x + Q_y dA = \int_0^1 \int_0^1 y-x dx dy = 0$$

      mark