Review for quiz 1

We have our first quiz next Friday, August 29th. This problem sheet represents most of the problems that will be on the quiz, though, I might add a problem after Monday’s class.

Problems

1. Curious about the following limit, \[ \lim_{x\to0} (1+x)^{3/x}, \] I used my computer to plug in several values of \(x\) that are close to \(0\) but not equal to \(0\). The results are shown in Table 1 below.

Table 1: Values of \(f(x)=(1+x)^{3/x}\) near \(x=0\).

\(x\)	0.100000	0.010000	0.001000	0.000100	0.000010
\(f(x)\)	17.449402	19.788466	20.055451	20.082525	20.085236

Based on those computations, can you make a conjecture as to the approximate value of the limit?
Be sure to indicate how many digits you believe to be correct and why.

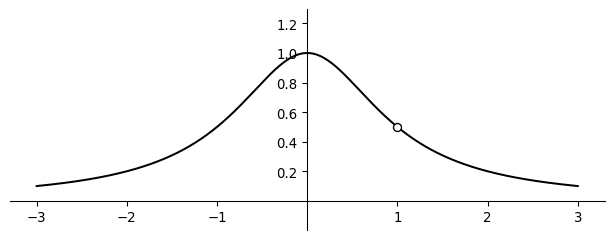
2. The graph of \[ f(x) = \frac{x-1}{x^3-x^2+x-1} \] is shown in Figure 1.

   1. Judging from the figure, what do you suppose is the value of \(\lim_{x\to1} f(x)\)?
   2. Use a little algebra together with the limit laws to prove that your guess is correct.

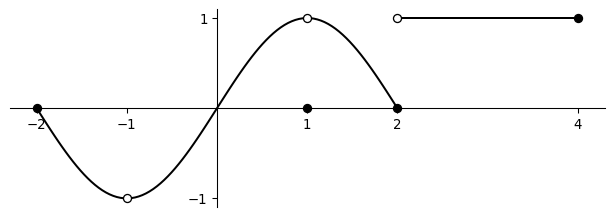
3. The Complete graph of a function \(f\) is shown in Figure 2. At each of the points \(a = −1\), \(a = 1\), \(a = 2\) and \(a = 4\), find the value of

   1. \(f(a)\),
   2. \(\lim_{x\to a^-}f(x)\),
   3. \(\lim_{x\to a^+}f(x)\), and
   4. \(\lim_{x\to a}f(x)\).

4. Compute the following limits.

   1. \(\displaystyle \lim_{x\to2}\frac{2x^2-3x-2}{x-2}\)
   2. \(\displaystyle \lim_{x\to1}\frac{x-1}{x^3+x-2}\)

Figures

Figure 1: The graph of \(f(x)=(x-1)/(x^3-x^2+x-1)\)

Figure 2: A graph for limits

Questions

If you’d like to ask a question about or reply to a question on this sheet, you can do so by pressing the “Reply on Discourse” button below.

embedDiscourseMathTopic(23)

import {embedDiscourseMathTopic} from '/components/EmbedDiscourseMathTopics/embedDiscourseMathTopic.js';