Numerically solve an IVP
(10 pts)
Produce and IVP of the form
$$
y' = r\,y\,\sin(y), : y(0)=1
$$
by choosing the decimals of $r$ to be the positions in the alphabet of your login name.
For example, my login name is mark and the positions of those letters are 13, 1, 18, and 11. Thus, for me, $r=0.1311811$ and my ODE is
$$
y' = 0.1311811 \, y \, \sin(y).
$$
Find the value of $t$ for which $y(t)=3$.
Comments
So, here's how I might approach it. First, my IVP is
$$
y' = 0.1311811 \, y \, \sin(y), \: y(0) = 1.
$$
OK, so first I'm going to load the libraries:
Now, let's set up and solve the IVP:
# Redefine f as a function of both y and t def f(y,t): return 0.1311811*y*np.sin(y) # Some t values that are appropriate to plot the solution t = np.linspace(0,20,100) # Solve it! y = odeint(f, 1, t).flatten() # Plot it!! plt.plot(t,y);Finally, I'll interpolate the solution and solve it:
``So my equation (if I use Chris as my name) is: $$ y' = 0.3818919 \, y \, \sin(y), \: y(0) = 1 $$
My code libraries are:
Then I set up and solved the IVP:
Finally, I interpolated the solution:
And got:
My IVP was: $$y' = (0.112935)\,y\,\sin(y), : y(0)=1$$
Loading the libraries:
Now for solving the IVP:
Interpolating the solution:
checking graphically:
My equation is:
$$ y' = 0.1020815135ysin(y) $$
Here's the code I did:
# A graphics library import matplotlib.pyplot as plt # Basic numerical tools import numpy as np # Scipy's numerical ODE solver from scipy.integrate import odeint # Convert data generated by odeint to a computable function from scipy.interpolate import interp1d # A numerical rootfinder from scipy.optimize import brentq # Redefine f as a function of both y and t def f(y,t): return 0.1020815135*y*np.sin(y) # Some t values that are appropriate to plot the solution t = np.linspace(0,20,200) # Solve it! y = odeint(f, 1, t).flatten() # Plot it!! plt.plot(t,y);array([1. , 1.00869456, 1.01751339, 1.02645847, 1.03553176,
1.04473522, 1.0540708 , 1.06354048])
array(3.10782519)
15.41536137275634
array(3.)
My IVP was
$$dy/dt=0.42512114y\sin(y), y(0)=1$$
Using basic, large step-size Euler's method, I got that at $$y(t)=3, t\approx3.62$$
To get a more precise estimate, I used Mark's code:
# A graphics library import matplotlib.pyplot as plt # Basic numerical tools import numpy as np # Scipy's numerical ODE solver from scipy.integrate import odeint def f(y,t): return 0.42512114*y*np.sin(y) t = np.linspace(0,8,100) y = odeint(f, 1, t).flatten() y plt.plot(t,y)To find that at $$y(t)=3, t\approx3.702112268685581$$
My IVP using my name Austin is:
$$y' = 0.1311811 \, y \, \sin(y), : y(0) = 1.$$
Next I loaded the libraries:
Then I solved the IVP:
# Redefine f as a function of both y and t def f(y,t): return 0.1211920914*y*np.sin(y) # Some t values that are appropriate to plot the solution t = np.linspace(0,20,100) # Solve it! y = odeint(f, 1, t).flatten() # Plot it!! plt.plot(t,y);Finally I interpolated the solution and solved it:
My IVP is:
$y^{\prime}=.114418523 y \sin (y), y(0)=1$
And my code and resulting answers are as follows:
Import necessary libraries:
import matplotlib.pyplot as pltimport numpy as npfrom scipy.integrate import odeintfrom scipy.interpolate import interp1dfrom scipy.optimize import brentqdef f(y,t):return .114418523*y*np.sin(y)t = np.linspace(0,20,100)y = odeint(f, 1, t).flatten()yThis gives me the array:
array([1. , 1.01976475, 1.04017289, 1.06124679, 1.08300904,
1.10548228, 1.12868906, 1.15265169, 1.17739199, 1.20293107,
1.2292891 , 1.25648492, 1.28453576, 1.31345679, 1.34326076,
1.37395749, 1.40555336, 1.43805078, 1.47144761, 1.5057366 ,
1.54090478, 1.57693284, 1.61379466, 1.65145672, 1.68987771,
1.72900818, 1.7687903 , 1.80915783, 1.85003621, 1.8913428 ,
1.9329875 , 1.97487337, 2.01689757, 2.05895252, 2.10092721,
2.14270855, 2.18418305, 2.22523826, 2.26576451, 2.30565631,
2.34481388, 2.38314434, 2.42056288, 2.45699355, 2.49236994,
2.52663557, 2.55974407, 2.59165907, 2.62235406, 2.65181188,
2.68002421, 2.70699093, 2.73271937, 2.75722353, 2.78052327,
2.80264357, 2.82361368, 2.84346643, 2.86223752, 2.87996487,
2.89668801, 2.91244763, 2.92728501, 2.94124171, 2.95435914,
2.96667832, 2.97823957, 2.98908237, 2.99924512, 3.00876505,
3.01767815, 3.026019 , 3.03382083, 3.04111539, 3.04793301,
3.0543026 , 3.06025159, 3.06580604, 3.07099064, 3.07582871,
3.08034231, 3.08455224, 3.08847808, 3.0921383 , 3.09555024,
3.0987302 , 3.10169349, 3.10445446, 3.1070266 , 3.1094225 ,
3.11165399, 3.11373212, 3.11566724, 3.11746902, 3.11914651,
3.12070814, 3.12216183, 3.12351492, 3.12477431, 3.12594641])
plt.plot(t,y)y_func = interp1d(t,y)t1 = brentq(lambda t: y_func(t)-1,0,20)t10.0plt.plot(t,y)plt.plot([t1,t1],[0,1.2],'k--')plt.plot(t1,1,'ko')IVP:
$$
y\prime = 0.11475121ysin(y)
$$
Load the Libraries:
Set up and solve the IVP:
Interpolate the solution and solve:
My equation is (using mcespede):
$$ y'=0.13351916545 y \sin (y) $$
My library codes are:
Then I set up and and solved the IVP:
# Redefine f as a function of both y and t def f(y,t): return 0.13351916545*y*np.sin(y) # Some t values that are appropriate to plot the solution t = np.linspace(0,20,100) # Solve it! y = odeint(f, 1, t).flatten() # Plot it!! plt.plot(t,y);Interpolate the solution and solve it:
# Output:
11.787222349796691
My equation is: $y' = (0.11255) * y * sin(y) $
Next I load the libraries:
Next setting up and solving the IVP
Finally, Interpolating the solution to solve
The output being
13.982315772416888
My equation is: $$y' = 0.51893y\sin(y)$$
First the following libraries are loaded:
Next the solution is graphed with the following code:
# Redefine f as a function of both y and t def f(y,t): return 0.51893*y*np.sin(y) # Some t values that are appropriate to plot the solution t = np.linspace(0,5,1000) # Solve it! y = odeint(f, 1, t).flatten() # Plot it!! plt.plot(t,y);Finally interpolating the solution using:
Output: 3.0323732170171915
Displaying this graphically:
Using my name generates my equation as:
$$y' = 0.1920516 \, y \, \sin(y), : y(0) = 1$$
Loading my libraries:
import matplotlib.pyplot as plt import numpy as np from scipy.integrate import odeint from scipy.interpolate import interp1d from scipy.optimize import brentqSolving the IVP:
def f(y,t): return 0.1920516*y*np.sin(y) t = np.linspace(0,12,100) y = odeint(f, 1, t).flatten() plt.plot(t,y);Finally, interpolating the solution and solving:
t0 = brentq(lambda y: y_interp(y)-3, 0, 12) t0Resulting in:
8.194529565299755
@ChristianDonaldson , @andrew , @Austin , @StephenC
I think you've all got some good work here but need a little help with formatting. Keep in mind that formatting is done with Markdown, as described in [this forum post]. In particular, a block of code should should be indented four spaces to appear as a code block in your post. For example, if we want to our post to look like:
def f(x): a = 2 return x+a f(3) # Output: # 5I'd type:
def f(x): a = 2 return x+a f(3) # Output: # 5Note that I've include the output as a Python comment.
You folks are using backticks to indicate code but that is meant for inline code. For example, if I wanted to write: Use the
defstatement to define a function, I'd just wrap the "def" in backticks. Note that inline code doesn't preserve linebreaks, which i why you all are having problems with that.SAM: 19,1,13
$r = .19113$
$$y'=.19113ysin(y)$$
# A graphics library import matplotlib.pyplot as plt # Basic numerical tools import numpy as np # Scipy's numerical ODE solver from scipy.integrate import odeint # Convert data generated by odeint to a computable function from scipy.interpolate import interp1d # A numerical rootfinder from scipy.optimize import brentq # Redefine f as a function of both y and t def f(y,t): return .19113*y*np.sin(y) # Some t values that are appropriate to plot the solution t = np.linspace(0,20,1000) # Solve it! y = odeint(f, 1, t).flatten() # Plot it!! plt.plot(t,y);array([[1. ],
[1.00322837],
[1.00647386],
[1.00973657],
[1.01301659],
[1.01631402],
[1.01962897],
[1.02296157]])
array([1. , 1.00322837, 1.00647386, 1.00973657, 1.01301659,
1.01631402, 1.01962897, 1.02296157])
array(3.1414658)
array(3.1414658)
8.23309851814031 -This is our solution
array(3.) -Checking
Based on my forum username "Badler" my personal IVP is:
$$y'=0.21412517ysin(y), y(0)=1$$
Where $$ r=0.21412517 $$
First I'm going to load the libraries:
Now I'll set up the IVP:
# Redefine f as a function of both y and t def f(y,t): return 0.21412517*y*np.sin(y) # Some t values that are appropriate to plot the solution t = np.linspace(0,10,100) # Solve it! y = odeint(f, 1, t).flatten() # Plot it!! plt.plot(t,y);Now I will interpolate and solve:
My login name is Jules so my numbers are 10, 21, 12, 5, and 19. Thus, my $r=0.102112519.$ So, my ODE is $$ y'=0.102112519ysin(y).$$
Now, let's set up and solve the IVP:
Redefine f as a function of both y and t def f(y,t): return 0.102112519*y*np.sin(y) Some t values that are appropriate to plot the solution t = np.linspace(0,20,100) # Solve it! y = odeint(f, 1, t).flatten() # Plot it!! plt.plot(t,y);Finally, I'll interpolate the solution and solve it:
From "max" I obtained the IVP
$$
y' = 0.13124ysin(y), y(0)=1.
$$
First load the libraries:
Then define the IVP and get a numeric solution:
# Redefine f as a function of both y and t def f(y,t): return 0.13124*y*np.sin(y) # Some t values that are appropriate to plot the solution t = np.linspace(0,20,1000) # Solve it! y = odeint(f, 1, t).flatten() # Plot it!! plt.plot(t,y);Now we interpolate the solution and then find $t$ in $y(t)=3$:
This code produces the output
11.99016421201848So $y(t)=3$ at $t=11.99016421201848$
This is further verified by running
y_interp(t0), which outputsarray(3.)My IVP is
$$y^1= 0.191181ysin(y), y(0) = 1. $$
First I need to load the libraries:
Now I'm going to set up and solve the IVP:
def f(y,t): return 0.191181*(y)*np.sin(y) t = np.linspace(0,20,100) y = odeint(f, 1, t).flatten() y plt.plot(t,y)My final output is found by the following code:
So our final output is 8.232968014338422
My IVP is:
$$y' = 0.1651818914y\sin y; y(0) = 1$$
Load libraries:
Set up and solve the IVP:
# Redefine f as a function of both y and t def f(y,t): return 0.1651818914 * y * np.sin(y) t = np.linspace(0, 20, 100) y = odeint(f, 1, t).flatten() plt.plot(t,y)Interpolate the solution, solve, and visualize:
Load Library
# A graphics library
import matplotlib.pyplot as plt
# Basic numerical tools
import numpy as np
# Scipy's numerical ODE solver
from scipy.integrate import odeint
# Convert data generated by odeint to a computable function
from scipy.interpolate import interp1d
# A numerical rootfinder
from scipy.optimize import brentq
Set up and solve the equation
# Redefine f as a function of both y and t
def f(y,t):
return 0.23977514152120ynp.sin(y)
# Some t values that are appropriate to plot the solution
t = np.linspace(0,10,100)
# Solve it!
y = odeint(f, 1, t).flatten()
# Plot it!!
plt.plot(t,y);
# Some t values that are appropriate to plot the solution
t = np.linspace(0,10,100)
# Solve it!
y = odeint(f, 1, t).flatten()
# Plot it!!
plt.plot(t,y);
Interpolate, solve and visualize
y_interp = interp1d(t,y)
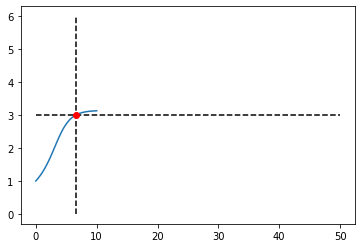
y_interp
t0 = brentq(lambda y: y_interp(y)-3, 0, 10)
t0
#output: 6.562862752442042
plt.plot(t,y)
plt.plot([t0,t0],[0,6],'k--')
plt.plot([0,50],[3,3],'k--')
plt.plot(t0,3,'ro');
@Wiggenout You should indent anything that you want to appear as a code block four spaces. Have a look at this post and the references therein.