Your favorite formula
(5pts)
I assume that you couldn't have made it this far into mathematics without having a favorite formula! So, share yours with the world responding to this post below. Be sure to:
- Typeset your formula using a LaTeX snippet and
- say something about where your formula comes from.
You might even include a picture, if appropriate!
For example:
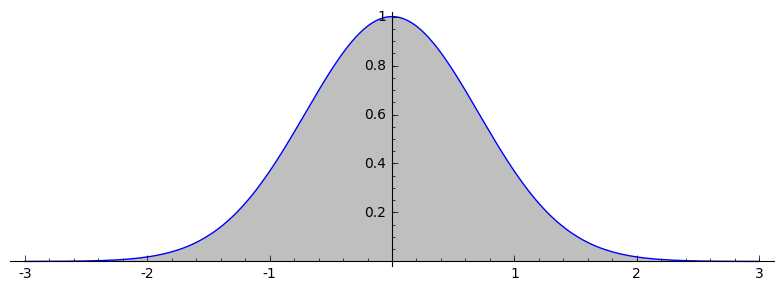
My favorite formula is the computation of the Gaussian integral:
$$\int_{-\infty}^{\infty} e^{-x^2} dx = \sqrt{\pi}.$$
This integral is extremely important in probability and statistics. In fact, if we normalize the integrand to get $e^{-x^2/2}/\sqrt{2\pi}$, we get the the normal distribution.
Geometrically, the formula states the the area under the curve below is one:
Here's what I typed in to get this:
My favorite formula is the computation of the
[Gaussian integral](https://en.wikipedia.org/wiki/Gaussian_integral):
$$\int_{-\infty}^{\infty} e^{-x^2} dx = \sqrt{\pi}.$$
This integral is *extremely* important in probability and statistics.
In fact, if we normalize the integrand to get $e^{-x^2/2}/\sqrt{2\pi}$,
we get the the normal distribution.
Geometrically, the formula states the the area under the curve below is one:

Note that last line was put in automatically by the image uploader.
Comments
My favorite formula is the classic Pythagorean Theorem: $$a^2+b^2=c^2$$
This is a fundamental formula in math as it helps you find side lengths of right triangles. Since right angles appear everywhere in buildings, this idea is crucial in construction. Also, it was only a few years ago in Calc 1 that I saw a visualization of the Pythagorean Theorem (pic below). I thought it was an interesting way to think about something that has become left behind at this point in our math careers.
My favorite formula (though I used to despise it) is the cantilevered beam formula from Castigliano's Theorem:
$$\delta = \frac{\partial}{\partial P} \int_{0}^{L} \frac{(Px)^2}{2EI} dx$$
This is a neat formula because it combines the methods of statics and material science. The purpose of this formula is to find the displacement of a point on a beam given a specific load or combinations of loads. Here's what problems typically look like:
My favorite formula is Euler's identity.
$$e^{i\pi}+1=0$$
Many consider it an example of great mathematical beauty. Here is the Wikipedia link. It combines five key mathematical concepts, the numbers $0$ and $1$, $\pi$, $e$, and the imaginary $i$. I first read about it earlier this year in the wonderful book "Zero: The Biography of a Dangerous Idea" by Charles Seife.
Even more interesting is that this summer I hike the 220 mile Camino Primativo in Northern Spain and it was grafitii'd in numerous places along the trail. It's hard to beat beautiful math combined with beautiful countryside.
Ohm's law is a neat one.
$$I = {V\over R}$$
It's the function we use to model the relationship between resistance, voltage, and current. It's one of those simple equations that a lot of heavier math in EE ends up being built on.
My favorite formula is the definition of the Laplace Transform:
$$F(s) = \mathcal{L} [f(t)] = \int_{0}^{\infty} f(t) e^{-st} dt$$
This transform is widely used in circuit analysis and control theory. It transforms functions from the time domain into the s domain. This is useful to describe the behavior of circuits and signals using transfer functions.
My favorite formula is actually quite a simple one. It's the formula for converting Fahrenheit to celsius:
$$C=\frac{5}{9}(F-32)$$
This formula is useful for when you might be talking to someone outside the country or when you use temperature in a scientific setting. I used this formula a lot this summer while talking to my international friends.
My Favorite Formula is the explicit formula for the Fibonacci sequence(i.e. the sequence starting with 1,1,2,3,5,8.... where each term is the sum of the previous two terms):
$$\frac{(\frac{1+\sqrt5}{2})^n-(-\frac{\sqrt5-1}{2})^n}{\sqrt5}$$
I find this formula interesting because the Fibonacci sequence is a very useful sequence, modelling many things in nature from the lineage of bees to pineapples, and this formula helps you to calculate large Fibonacci numbers easily.
My favorite formula would probably be the taylor series:
$$f(x) = \sum_{n=0}^{\infty} \frac{f^{n}(a)}{n!} (x-a)^{n}$$
I just think it is super cool that we can approximate many functions accurately with polynomials generated by a series. Power series such as the taylor series are useful in the realm of computer science and engineering as it is much more resource efficient to approximate a complex function with a long polynomial.
My favorite formula (so far) is Schrodinger's 1-D Time-Dependent equation.
$$-\dfrac{\hslash^2}{2m} \, \dfrac{\partial ^2 \psi}{\partial x^2}+V {\psi}=i{\hslash} \dfrac{\partial \psi}{\partial t}.$$
This equation determines the wave function ${\psi(x,t)}$ of a particle for all future time. The wave function ${\psi}$ is a "complex-valued probability amplitude". It is the probability of finding a particle in a space set.
One of the coolest formulas that I've learned about is the
Schwarschild radius formula:
$$R_{g}=\frac{2GM}{c^2}$$
where $G$ is the gravitational constant and $c$ is the speed of light.
This formula links the mass of a black hole with the radius of its event horizon, where even light cannot escape the black hole's gravity. It's an important formula in astrophysics, and it blew my mind how simple it is!
My favorite formula would have to be the Predator and Prey model...
x′ = a x − αxy
y′ = −c y + γxy
This has to be one of the most interesting formulas that I learned in DFQ. I am an ENVR Science major and to see Math and environment factors connect is very cool. This formula is also very simple but is able to model so of the most inherent factors that balance the ecosystems that are functioning around us. I also like the fluidity in the ability to add contributing factors (i.e. climate change, invasive species) into these types of formulas and model the outcomes.
Maybe because I just learned it or maybe because it is derived from the two laws, Charles' and Boyle's law (Brooklyn 99?), my favorite formula is the equation of state for an ideal gas:
$$p\alpha = RT$$
where $p$ is pressure, $\alpha$ is specific volume, $R$ is a gas constant, and $T$ is temperature. This formula is important because it shows the relationship between the three variables: pressure, specific volume, and temperature, and because it is written in such a way that you do not need to know the actual mass of a sample. This is useful in thermodynamics because you can study the characteristics of small and large amounts of a fluid with the same formula.
One of my favorite formulas is the expression for the energy of a body in special relativity. Many people have heard about $E = mc^2$. It is one of the world's most iconic equations, but is actually just a part of a more complete equation:
$$E^2 = m^2c^4 + p^2c^2$$
This can account for the energy of photons (which have momentum, but no mass) and also kinetic energy. A really cool fact about it is if you think of $E$ as a function of $p$ and do the first three terms of its Maclaurin series expansion, you get $mc^2 + \frac{p^2}{2m}$. Using the definition $p = mv$, $\frac{p^2}{2m} = \frac{1}{2}mv^2$, which is the formula for kinetic energy in basic physics. This shows that the normal kinetic energy formula is really just an approximation of the energy equation in relativity.
My favorite formulas are actually two that are somewhat related.
The first one is the Harmonic Series, which states that:
$$\sum_{n=1}^{\infty} \frac{1}{n} = 1 + \frac{1}{2} + \frac{1}{3} + \frac{1}{4} + \frac{1}{5} + ... = \infty$$
While that on its own is cool, the fact that the summation of a series of infinitely decreasing numbers still goes to infinity, there is something else that I find really cool.
If you square the denominator you get the Basel Problem which does converge to:
$$\sum_{n=1}^{\infty} \frac{1}{n^2} = 1 + \frac{1}{4} + \frac{1}{9} + \frac{1}{16} + \frac{1}{25} + ... = \frac{\pi^2}{6}$$
I just find it pretty cool that something as simple as squaring the denominator changes the divergent series into a convergent series.
My favorite formula is the derivative power rule:
$$f(x)=x^{n}$$
$$f'(x)=nx^{n-1}$$
This is highly nostalgic. I was excited when I first learned the formula because it felt like reaching the culmination of my long algebra career... opening up a new world: calculus.
My favorite formula is Gauss's Law for Electric Flux, one of Maxwell's Equations for electromagnetism. These equations form the basis for all of classical electrodynamics. Gauss's Law states:
$$\Phi_E=\oint \vec{\textbf{E}}\cdot d\vec{A}=\frac{Q}{\mathcal{E}_0}$$
In other words, the net electric flux $\Phi_E$ through a closed surface is equal to the enclosed charge $Q$ divided by the Electric Constant $\mathcal{E}_0$.
My favorite formula describes the effect of Rayleigh Scattering:

$$\frac{I}{I_0}=\frac{8{\pi}{N}\alpha^{2}}{\lambda^{4}r^{2}}(1+\cos^{2}(\theta)).$$
This formula is useful to describe the elastic effect of the scattering of light when a molecule absorbs a photon and immediately readmits the photon. This technique is sometimes used to calculation concentrations of chemical materials, but it also describes why the sky is blue during the day. Since the lambda describes the wavelength of visible light, blue, which has the shortest wavelength, would have the highest intensity and scatter more effectively in the sky.
My favorite formula is the quadratic formula.
$$x=\frac{-b\pm\sqrt{b^2-4ac}}{2a}.$$
This is my favorite formula because the formula will get the values of x that solve a quadratic equation every time without fail. I really like how systematic and sometimes tedious the formula can be to solve. The certainty that comes with the quadratic formula is another aspect that I really enjoy. This formula is always a useful one to know and I have encountered it many times throughout my mathematic career.
My favorite equation is the equation of motion for a harmonic oscillator. This equation is based on Newton's Second Law (F=ma) and utilizes the forces acting on an object (c is the damping coefficient while k is the spring constant) in order to form the characteristic equation (typically using a solution in the form $y(t)=C e^{st}$) $ms^2 +cs + k =0$, which allows you to solve for the coefficients $s_1$ and $s_2$ using the quadratic formula. This results in the solutions $ y_1(t)=C_1 e^{s_1(t)}$ and $y_2(t)=C_2 e^{s_2(t)}$, where $C_1$ and $C_2$ are found after setting initial conditions.
$$ m\ddot y(t) + c\dot y(t) + ky(t) = 0$$
One of my favorite functions is the gamma function:
$$(n-1)! = \int_{0}^{\infty}x^{n-1}e^{-x} dx$$
While it has many applications across mathematics, it is most famous for extending the definition of factorials. While the ordinary formula of $n! = n(n-1)(n-2)...1$ only works for positive integers, this function allows us to calculate the factorial of a negative or fractional number. I think its a very neat example of the power of mathematics and specifically calculus.
(testing amsmath package - works!) I'll give a meteorological formula popular in the storm chasing community - the fixed significant tornado parameter (sigtor, STP). It is a culmination of favorable atmospheric conditions and ingredients most likely to support significant and/or violent (EF2-EF5) tornadoes spawned by supercells:
$$\text{sigtor} = (\frac{\text{sbCAPE}}{1500\text{Jkg}^{-1}})(\frac{200+\text{sbCIN}}{150\text{Jkg}^{-1}})(\frac{\text{SRH}}{150\text{m}^2\text{s}^{-2}})(\frac{\text{BWD}}{20\text{ms}^{-1}})(\frac{2000-\text{sbLCL}}{1000\text{m}}),$$
where sbCAPE is the surface-based convective available potential energy in J/kg (how much energy an air parcel would gain by rising to a point in the atmosphere, beginning from the surface); sbCIN is the surface-based convective inhibition in J/kg (a sort of "cap" in the atmosphere that requires a storm to have a strong enough updraft to break through and become a mature cell); SRH is the 0-1km storm relative helicity in m^2/s^2, or the tendency for the storm to rotate, which is a key factor in defining a supercellular storm; BWD is the 0-6km bulk wind difference in m/s, also known as vertical wind shear where wind changes in speed and direction with height; and sbLCL is the surface-based Lifted Condensation Level (LCL) in meters, which is at a height equivalent to the base of a cloud you see when you look up at the sky.
All of these terms are rounded for certain value ranges (i.e. sbLCL term = 1.0 for $ \text{sbLCL} <1000 \text{m}$, 0.0 for $\text{sbLCL}>2000\text{m}$). Thus, every term must be sufficient enough to support tornadic development, otherwise the STP will be 0. The range we are looking for is $\text{sigtor}>1$ to indicate the feasibility of a supercell producing a strong or violent tornado in a given area. The area is usually defined within multiple locations that have taken atmospheric readings via rawinsonde, or atmospheric models forecasting areas where these favorable conditions will be present.
Below is an example of STP values exceeding 6 in Iowa from July 2017:
My favorite formula is the Newton's Law of cooling formula: $$T(t)=T_s+{(T_o-T_s)}e^{-kt}.$$
$T(t)$ is the temperature of the body at time t
$T_s$ is the surrounding temperature
$T_o$ is the initial temperature of the object
$k$ is a cooling constant specific to the object
The greater the difference between the surrounding temp and the body, the more rapid the temperature changes.
We all know that the greatest formula is the first part of the Fundamental Theorem of Calculus:
$$\int_{a}^{b} f(x)dx = F(b)-F(a)$$
Where $f$ is continuous on $[a,b]$ and $F$ is the indefinite integral of $f$ on $[a,b]$.
This is great because it actually allows human beings to compute integrals. We are all traumatized by Reimann sums in Calculus one for the specific purpose of making us appreciate this formula. Newton cracked this most likely around 1666, although it took several decades to be published, first by Leibniz. The public availability of this brilliant, simplified method of calculating integrals gave engineers and physicists a massive step forward into the industrial revolution.
My favorite equation is a simple one, the number e.
In the 17th century Jacob Bernoulli was looking into compound interest, specifically compounding intervals. He took the limit of the compound interest formula, $$\lim_{n\to\infty} (1+1/n)^n$$ for a 1 dollar account and found it resulted in an irrational number 2.718...or e.
It can also be written as the series:
$$\sum_{n=0}^{\infty} 1/n!$$
The discovery of one of the most useful constants in all of mathematics was just happenstance. I love that mathematical discoveries like this are oftentimes accidents, it gives a real sense of mystery to the subject...who knows what's out there, waiting to be stumbled upon.
My favorite equation is a frequently used equation in chemistry:
$$PV=nRT$$
The Ideal Gas Law is an equation to see what is the state of a hypothetical gas with:
P is the pressure of the gas
V is the volume
n is the amount of gas in moles
R is the ideal gas constant
T is the temperature in kelvin
One can use this equation to figure out the approximate state of a gas in given condition.
My favorite formula is the Ideal Gas Law:
$$PV = nRT$$
$P$ is equal to pressure ($atm$)
$V$ is equal to volume ($m^{3}$)
$n$ is equal to the number of moles of gas ($mol$)
$R$ is equal to the ideal gas constant ($8.3145 J * mol^{-1} * K^{-1}$)
$T$ is equal to the temperature ($K$)
The Ideal Gas Law is a combination of three simpler gas laws—Boyle's Law, Charles's Law, and Avogadro's Law—and it is very useful in chemistry when calculating the unknown variables of ideal gases.
The picture above depicts the isotherms of an ideal gas, where each of the curved lines represents the relationship between the pressure and volume of an ideal gas at different temperatures.
My favorite formula is used to integrate by parts. It is probably not that exciting, but I like saying the little rhyme when I use it:
$\int{}^{} u dv = uv - \int{}^{} v du$
It is helpful when finding a solution to an integral where two functions are multiplied together.
This picture shows the graphical representation of the theorem:
My favorite formula is the definition of a derivative:
$f'(x)= \lim_{h\to 0}\frac{f(x+h)-f(x)}{h}$
I like this formula because it was one of the first ones we learned in Calc 1, and I really enjoyed that class (which is why I'm continuing to take more math classes).
Derivatives are also one of the fundamental tools of Calculus, and shows rate of change. It is the slope of the tangent line at one point on a graph. This picture from wiki illustrates this idea:
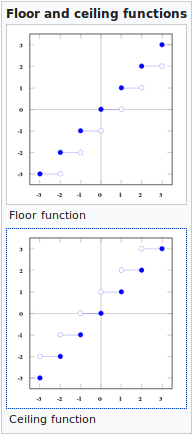
I don't have a favorite formula in particular but the floor and ceiling functions are neat. The floor function rounds down to the nearest integer and the ceiling function rounds up. They are useful in math and computer science when you are mapping from the real numbers to the integers. They are often times defined like this: $$ floor(x) = ⌊x⌋ $$ $$ ceil(x) = ⌈x⌉ $$
My favorite formula is an iconic and cliché one, a formula presented by Albert Einstein:
$$E=MC^2$$
This formula caused a paradigm shift in physics, as it related two things that were previously thought to be entirely without relationship to one another: light and mass. This formula defined special relativity as we know it today, and really demonstrated the powerful application math has in our modeling and understanding of the universe.