Revision history [back]

I agree with your solution Justin, and your computer program got the same answer as my 3d drafting program, lol. To find it mathematically we can deduce that the plane is halfway between the two circles, and the distance between the centers of the circles is the magnitude of the vector pointing from the center of the first to the center of the second. let $\vec w$ be equal to this vector and we find $$\vec w= \langle 1,1,1\rangle$$ Now we can find the distance from the center of the unit circle to the plane by taking half the magnitude of $\vec w$$$\frac{1}{2}\|\vec w\|=\frac{1}{2}\sqrt{1^2+1^2+1^2}=\frac{1}{2}\sqrt{3}$$
We also know that the distance form the origin to anywhere on the unit circle is the radius 1. puting these values into the graph below we see

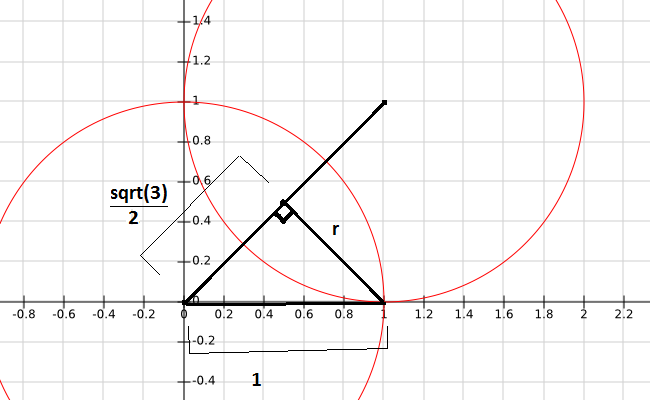
I didnt have a 3d program i could easly write over, so you have to ignore the 2 dimensional part, but it still allows us to see that to compute the radius we can use pythagorean theorem$$a^2+b^2=c^2\to a^2=c^2-b^2\to a=\sqrt{c^2-b^2}$$ Now substituting $a=r,b=\frac{\sqrt{3}}{2},c=1$ we get$$ r=\sqrt{1^2-\left(\frac{\sqrt{3}}{2}\right)^2}=\sqrt{1-\frac{3}{4}}=\sqrt\frac{1}{4}=\frac{1}{2}$$ Plugging this into your equation above we get an answer of $$\vec p(t) = \left\langle \frac{1}{2}, \frac{1}{2}, \frac{1}{2} \right\rangle + \frac{1}{2}\cos(t)\frac{\langle 0, 1, -1 \rangle}{\sqrt{2}} + \frac{1}{2}\sin(t)\frac{\langle 4, -2, -2 \rangle}{\sqrt{24}}$$