Revision history [back]

For starters, here's a groovy picture.

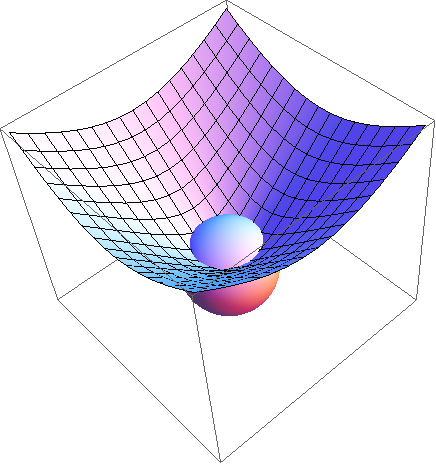
That image shows a sphere of radius 2 centered at the origin intersecting with the given cone. You can see that our integral with respect to $\rho$ will be from $0$ to $1$ since the cone continues down to its cusp at the origin.

Our integral with respect to theta will be from $0$ to $2 \pi$ since the rotation about the $z$-axis will have to be all the way around the section of the sphere above the cone.

Our integral with respect to $\rho$ will be from $0$ to $2$ since the sphere is of radius two.

So next you have to determine the angle from the "top" of the sphere to the inside surface of the cone. If you think about points that are on the cone in the $x$-$z$ plane a pattern becomes pretty apparent.

Points like $(1,0,1)$ and $(0,0,0)$ indicate that the surface of the cone is sloped at $45^{o}$ relative to the $x$-axis. Here's the same groovy plot including the parametrized line through the origin, $ \langle t,0,t \rangle.$

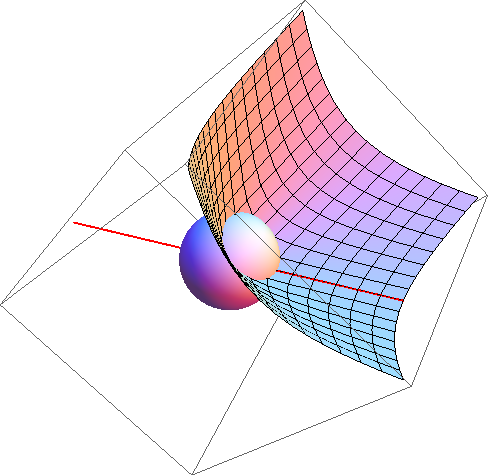
You can see that the line runs along the surface of the cone confirming the $45^{o}$ angle hypothesis.

So your integral is $$\int_{0}^{2 \pi} \int_{0}^{\frac{\pi}{4}} \int_{0}^{1} \rho ^{2} \rho^2 d \rho d \theta d \phi$$ $$=\int_{0}^{2 \pi} \int_{0}^{\frac{\pi}{4}} \int_{0}^{1} \rho ^{4} d \rho d \theta d \phi$$

Hopefully I haven't confused $\phi$ for $\theta$. Sorry if I did.

For starters, here's a groovy picture.

That image shows a sphere of radius 2 centered at the origin intersecting with the given cone. You can see that our integral with respect to $\rho$ will be from $0$ to $1$ since the cone continues down to its cusp at the origin.cone.

Our integral with respect to theta will be from $0$ to $2 \pi$ since the rotation about the $z$-axis will have to be all the way around the section of the sphere above the cone.

Our integral with respect to $\rho$ will be from $0$ to $2$ since the sphere is of radius two.

So next you have to determine the angle from the "top" of the sphere to the inside surface of the cone. If you think about points that are on the cone in the $x$-$z$ plane a pattern becomes pretty apparent.

Points like $(1,0,1)$ and $(0,0,0)$ indicate that the surface of the cone is sloped at $45^{o}$ relative to the $x$-axis. Here's the same groovy plot including the parametrized line through the origin, $ \langle t,0,t \rangle.$

You can see that the line runs along the surface of the cone confirming the $45^{o}$ angle hypothesis.

So your integral is $$\int_{0}^{2 \pi} \int_{0}^{\frac{\pi}{4}} \int_{0}^{1} \rho ^{2} \rho^2 d \rho d \theta d \phi$$ $$=\int_{0}^{2 \pi} \int_{0}^{\frac{\pi}{4}} \int_{0}^{1} \rho ^{4} d \rho d \theta d \phi$$

Hopefully I haven't confused $\phi$ for $\theta$. Sorry if I did.

For starters, here's a groovy picture.

That image shows a sphere of radius 2 centered at the origin intersecting with the given cone.

Our integral with respect to theta will be from $0$ to $2 \pi$ since the rotation about the $z$-axis will have to be all the way around the section of the sphere above the cone.

Our integral with respect to $\rho$ will be from $0$ to $2$ since the sphere is of radius two.

So next you have to determine the angle from the "top" of the sphere to the inside surface of the cone. If you think about points that are on the cone in the $x$-$z$ plane a pattern becomes pretty apparent.

Points like $(1,0,1)$ and $(0,0,0)$ indicate that the surface of the cone is sloped at $45^{o}$ relative to the $x$-axis. Here's the same groovy plot including the parametrized line through the origin, $ \langle t,0,t \rangle.$

You can see that the line runs along the surface of the cone confirming the $45^{o}$ angle hypothesis.

So your integral is $$\int_{0}^{2 \pi} \int_{0}^{\frac{\pi}{4}} \int_{0}^{1} \int_{0}^{2} \rho ^{2} \rho^2 d \rho d \theta d \phi$$ \phi d \theta$$ $$=\int_{0}^{2 \pi} \int_{0}^{\frac{\pi}{4}} \int_{0}^{1} \int_{0}^{2} \rho ^{4} d \rho d \theta d \phi$$\phi d \theta$$

Hopefully I haven't confused $\phi$ for $\theta$. Sorry if I did.