PDE - Review for Exam II

Here are some problems to play with for the exam on Wednesday.

  1. Find the full Fourier series of \(f(x)=x\) over the interval \([-1,1]\).

  2. Solve the heat problem \(u_t = u_{xx}\) on the interval \([0,\pi]\) subject to \(u(0,t)=u(\pi,t)=0\) and \(u(x,0)=x^2 \sin(x)\).
    Note: You may assume that \[\int_0^{\pi} x^2 \sin(x) \sin(n\pi x) \, dx = \begin{cases} - \frac{\pi}{4} + \frac{\pi^{3}}{6} & \text{for}\: n = 1 \\- \frac{4 \left(-1\right)^{n} \pi n}{n^{4} - 2 n^{2} + 1} & \text{otherwise} \end{cases}.\]

  3. Given two functions \(f\) and \(g\) continuous on the unit interval, define their inner product by \[\langle f,g\rangle =\int _0^{1}f(x)g(x)dx\] Given any three such functions \(f\), \(g\), and \(h\), prove that \[\langle f-g,h\rangle =\langle f,h\rangle -\langle g,h\rangle.\]

  4. Suppose you are asked to estimate the solution to the boundary value problem \[y'' + x^3 y = e^x \text{ subject to } y(0) = 0, y(2) = 1.\] You do so by breaking the interval \([0,2]\) into 4 equal pieces allowing you to approximate \(y''\) with the symmetric difference quotient for the second derivative. Write down the resulting linear system of equations that the \(y_i \approx y(x_i)\) must satisfy.

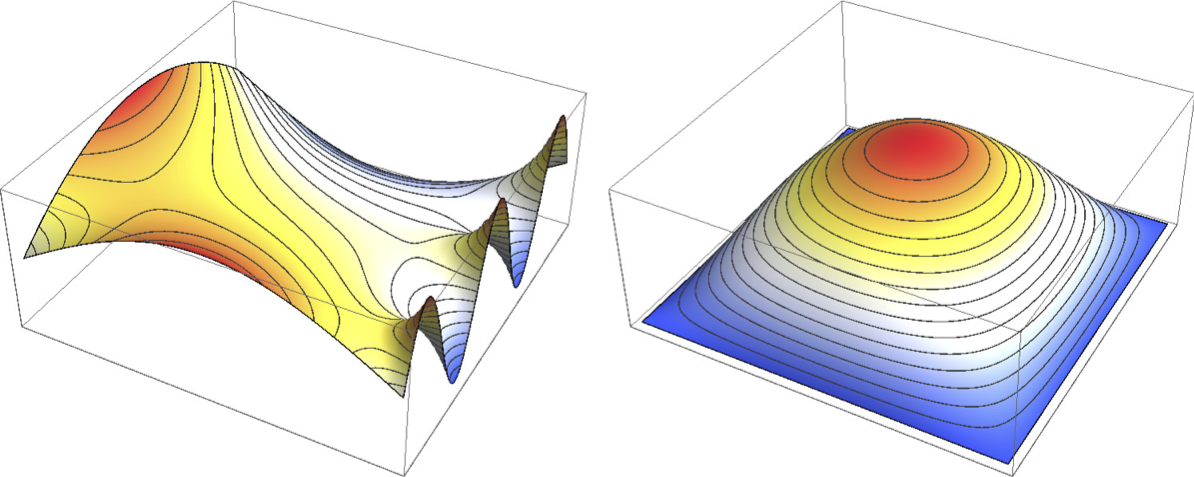
  1. The figure below shows the graph of two functions on the unit square. Which of these can be a solution of of Laplace’s equation \(\Delta u=0\). You must clearly state a property that \(u\) must satisfy that one graph clearly does not have in order to get full credit.

The graphs of two functions on the unit square