PDE - Review 1
Here are some problems to play with for the exam on Wednesday.
Consider the first order equation \(u_x-u_t=2x-t\).
Verify that \(u(x,t)=f(2x+t)-x t\) solves the equation sufficiently smooth function \(f\).
Use part (a) to solve the initial value problem \(u_x-u_t=2x-t\) subject to \(u(x,0)=e^{2x}\).
Express the first order equation \(u_x-u_y=u+x y\) in terms of the new variables \(\xi =2x+y\) and \(\psi =x-2y\).
A string of length one is held tightly at either end, making a straight line from \(x=0\) to \(x=1\). At time \(t=0\), we slap the string imparting an initial velocity of \(v(x)=-\sin (x)\) at each point \(x\) along the string. Write down a PDE description of the subsequent motion of the string, assuming that the density and tightness yield a string constant of \(c=1\).
The initial temperature of a bar of length one and diffusivity one is set to \(u_0(x)=\sqrt{x}\). The left end held temperature zero and the right end point is set to \(t/(1+t)\).
Write down a PDE description of this problem.
Are the boundary conditions consistent with the initial condition?
Sketch the solution \(u(x,t)\) as a function of \(x\) for \(t=0\), \(t=0.01\), \(t=0.1\), and \(t=10^{10}\).
Consider the equation \(2u_{x x}+u_{x y}+2u_{y y}+4u_xu_y+2u=2\).
Is this equation linear or non-linear?
Is this equation quasi-linear?
Is this equation parabolic, hyperbolic, or elliptic?
Solve the heat problem \(u_{t} = 2u_{xx}\) on \(\mathbb R\) subject to \[u(x,0) = \begin{cases} 1-x^2 & |x| < 1 \\ 0 & |x| > 1. \end{cases}\]
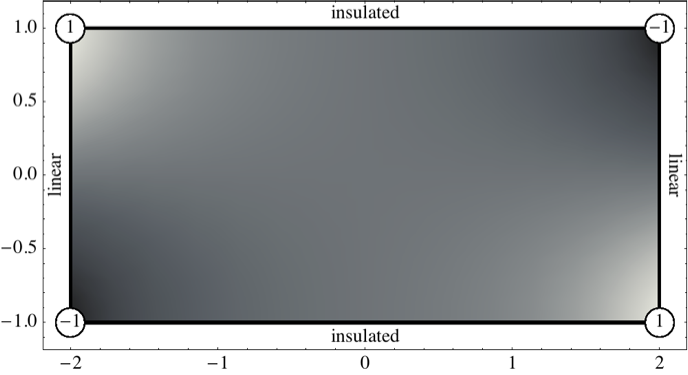
We consider a heat conduction problem on the rectangle \(-2\leq x\leq 2\), \(-1\leq y\leq 1\). The initial temperature distribution is identically zero throughout. At time \(t=0\), the temperature of the vertices are instantly set to either \(1\) or \(-1\) and the edges are either insulated or held at the constant temperature obtained via linear interpolation as indicated in Figure 1. Write down a PDE description of this problem.
Note: The shading in the figure illustrates the ultimate steady state temperature distribution. The problem is dynamic, however, so your solution will involve \(t\).