The wave equation

Suppose that describes the displacement from equilibrium of a vibrating string whose ends are fixed. The fundamental equation governing this motion is Let's look at the derivation of this 1D equation together with some simple solutions.

Derivation

The wave equation is essentially a consequence of Newton's second law. We assume that the string has a uniform linear density and constant tension . We then consider the motion of a small portion of the string over the interval from to . The vertical acceleration of this portion is due entirely to the vertical components of the tension in the string: and .

The total force on this portion of the string is the difference between these two components and, by Newton's second law, this total force must equal the mass of this portion times its acceleration. In symbols,

${tex.block`V(x+\Delta x,t)-V(x,t) = \rho \Delta x u_{tt}``}

or, dividing by ,

After taking a limit as , we get It turns out that the horizontal and vertical components of the tension at a point are related to one another via the slope of the string, : .

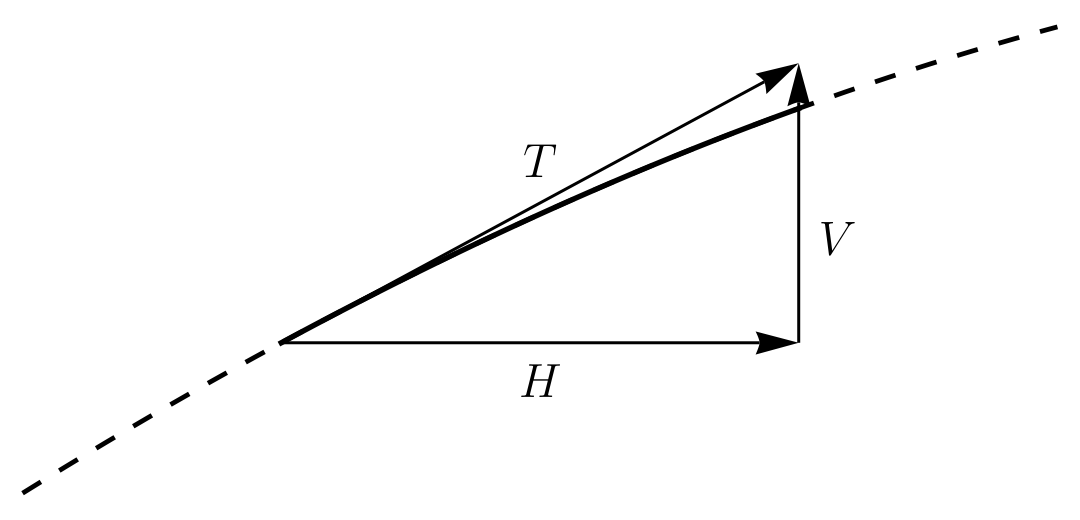
Assuming the displacement of the string is small, . Thus plugging for into we get the wave equation in the form