Final Practice Solutions

for Stat 185

Here are the solutions to the practice problems for next week's final exam.

Problem 1

Solution

As we know, the confidence interval should have the form $$\bar{x} \pm z^* SE,$$ where $\bar{x}=253.77$ is the computed mean and the standard error is the computed standard deviation divided by the sample size: $$SE = s/\sqrt{n} = 45.72/\sqrt{105} \approx 4.46$$ That last part is the solution to part (a).

Solution (cont)

To find $z^*$ for a $98\%$ confindence level, look for $(1-0.98)/2 = 0.01$ in the normal table. It looks like, we get a value between $2.32$ and $2.33$. (Either of those is fine, though I prefer to round up.)

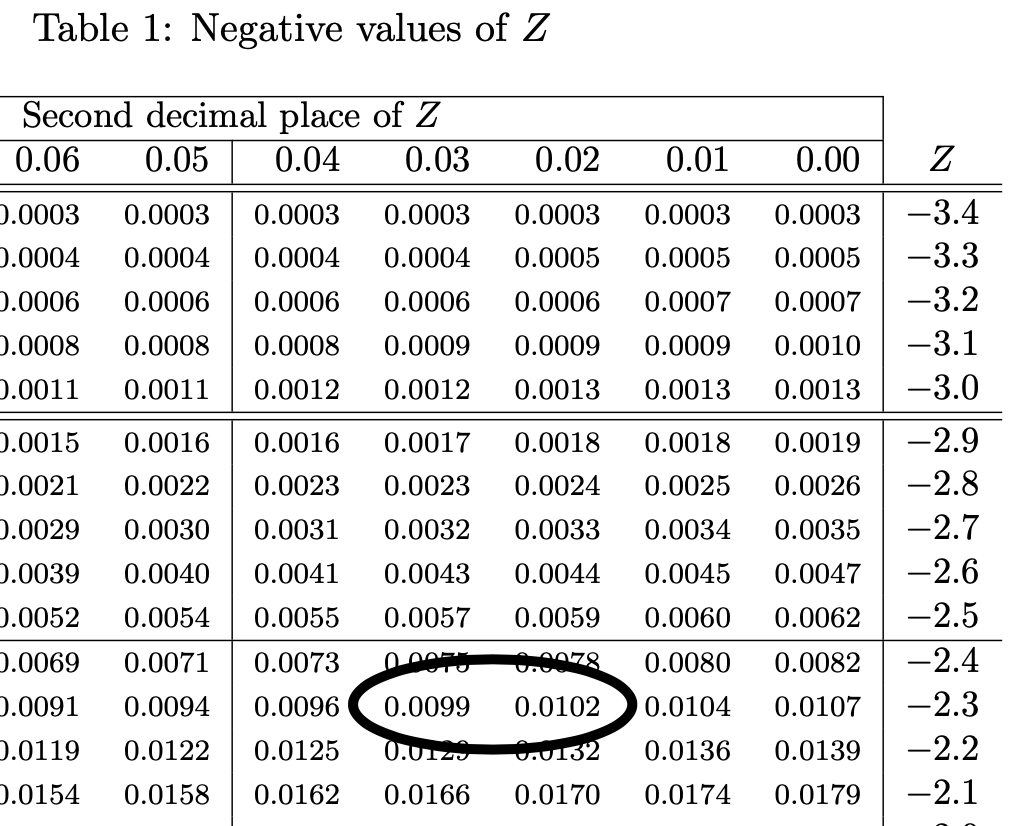
Solution wrap-up

For the final answer, we get

Problem 2

Solution for part (a)

The mean is $$\bar{x} = \frac{x_1 + x_2 + \cdots + x_n}{n} = \frac{273.8 + 203.5 + 259.4 +246.1}{4} = 245.7.$$

Solution for part (b)

The standard deviation is $$\begin{aligned} s &= \sqrt{\frac{(x_1 - \bar{x})^2 + (x_2 - \bar{x})^2 + \cdots + (x_n - \bar{x})^2}{n-1}} \\ &= \sqrt{\frac{(273.8 - 245.7)^2 + (203.5 - 245.7)^2 + (259.5 - 245.7)^2 + (246.1 - 245.7)^2}{3}} \\ &\approx 30.3373. \end{aligned}$$

Solution for part (c)

The standard error is $$SE = \frac{s}{\sqrt{n}} = \frac{30.3373}{\sqrt{4}} = 15.16.$$

Solution to part (d)

To write down the confidence interval, we'll need a $t^*$ multiplier, which we look up in our $t$-table. We find that for a a two-tailed significance of level of $0.05$, we'll need $t^*=3.18$:

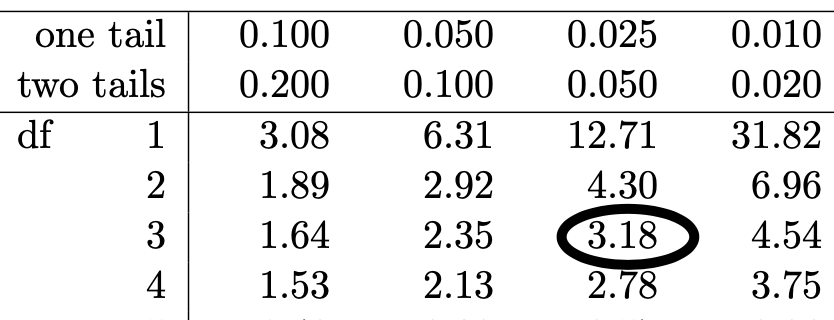
Solution to part (d) wrap-up

Finally, our confidence interval is $$\bar{x} \pm t^* \times SE = 245.7 \pm 3.18 \times 15.15.$$

Problem 3

Solution to part (a)

The hypothesis test is $$\begin{aligned} & H_0: p = 0.5 \\ & H_A: p < 0.5, \end{aligned}$$ where $p$ denotes the proportion of marathon runners who are women.

Solution to part (b)

The standard error is $$SE = \sqrt{\frac{p(1-p)}{n}} = \sqrt{\frac{0.5\times0.5}{1200}} \approx 0.0144.$$

Solution to part (c)

The test-statistic is $$T = \frac{\hat{p} - p}{SE} = \frac{\frac{507}{1200} - 0.5}{0.0144} \approx -5.38$$

To conclude the test, we'll clearly reject the null hypothesis with such an extreme test statistic.

Problem 4

Solution to part (a)

The hypothesis test is $$\begin{aligned} & H_0: \mu_{40} - \mu_{50} = 0 \\ & H_A: \mu_{40} - \mu_{50} < 0 \\ \end{aligned}$$ where $\mu_{40}$ denotes the average time of marathon runners in their 40s and $\mu_{50} denotes the average time of marathon runners in their 50s.

Solution for part (b)

The standard error is $$SE = \sqrt{\frac{s_{40}^2}{n_{40}} + \frac{s_{50}^2}{n_{50}}} = \sqrt{\frac{43.7^2}{7217} + \frac{44.7^2}{4156}} = 0.863.$$

Solution for part (c)

The test-statistic is $$\frac{\mu_{40}-\mu_{50}}{SE} = \frac{255.2-270.8}{0.863} = -18.0765.$$ We, again, immediately reject the null hypothesis.

Problem 5

Solution to part (a)

The hypothesis test is $$\begin{aligned} & H_0: \mu_{1} - \mu_{2} = 0 \\ & H_A: \mu_{1} - \mu_{2} < 0. \\ \end{aligned}$$

Solution for part (b)

The standard error is $$SE = s/\sqrt{n} = 32.7/\sqrt{59} = 4.257.$$

Solution for part (c)

The test statistic is $$\frac{\bar{x}-0}{SE} = \frac{26.1}{4.257} = 6.13.$$ Once again, we immediately reject the null.

Problem 6

The picture below shows a scatter plot for a random sample of 1200 runners in the Boston Marathon. The $x$-coordinate of each point corresponds to the runner's age and the $y$-coordinate corresponds to the runners time in minutes. The regression line for the data is also shown and has formula $y = 0.719x + 227.6.$

Problem 6 (statement continued)

1. What time does this regression model predict for a 56 year old runner?
2. Which of the following could be a reasonable value for the correlation between age and time: 0.9, 0.2, -0.2, or -0.9?
3. Suppose I run a linear regression test on this data and I get results like the following:

   LinregressResult(slope=0.71868458889427973,
     intercept=227.5951853339659, rvalue=0.258752071669993,
     pvalue=8.263097704087485e-20, stderr=0.13124270715070266)
   									

   Can I conclude at the 99% level of conficence that there is a linear relationship between age and speed?

Solution for part (a)

Simply plug the number $x=56$ into the regression formula to get a prediction of $$0.719\times56 + 227.6 = 267.864.$$

Solution for part (b)

The positive slope of the regression line indicates a positive relationship between the variables, which rules out the negative numbers. Given how scattered about the points are, I'd have to go with $0.2$ over $0.9$.

Solution for part (c)

The outrageously small $p$-value of

pvalue=8.263097704087485e-20