Multivariate CoV
Polar coordinates are one example of a change of variables in multivariate integration. Other important examples of this arise in triple integrals, including cylindrical and spherical coordinates. Before we do that, it might make sense to talk about change of variables in general.
An elliptic example
What is the volume below the graph of $f(x,y)=4-(x^2+4y^2)$ and over the $xy$-plane, as shown below?
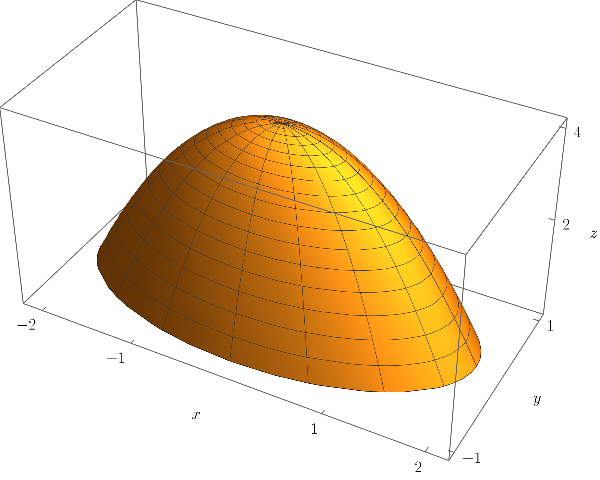
Note that this image is very similar to our first polar image.
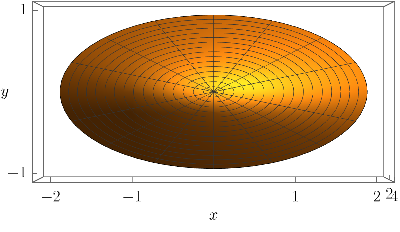
Elliptical example from above
When we look at this one from above, we see an ellipse:
Ellipse in the plane
Here's the ellipse $E$ in the plane (generated with this):
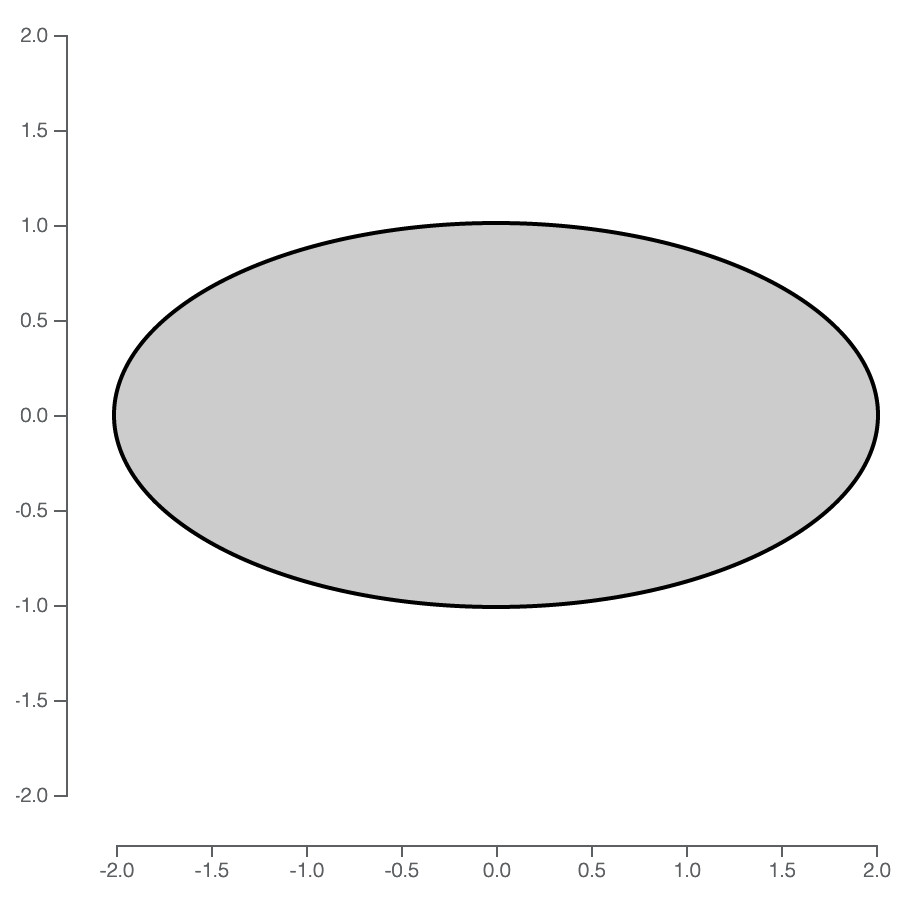
Then the volume is then $\displaystyle \iint_{E} \left(4-(x^2+4y^2)\right) dA.$
New coordinates
To describe that ellipse, I'm going to introduce new variables $s$ and $t$ by defining their relationship with $x$ and $y$:
$$\begin{align} x &= 2\,s\cos(t)\\ y &= s\sin(t). \end{align}$$For a fixed value of $s$, these equations parametrize an ellipse that's twice as wide as it is tall. For the set of all values of $s$ from zero to one, we trace out a solid ellipse.
New coordinates (cont)
Put another way, we might say that the parametric equations $$ x = 2\,s\cos(t), \: \: y = s\sin(t) $$ map the rectangle $[0,1]\times[0,2\pi]$ in the $st$-plane to the ellipse in the $xy$-plane.
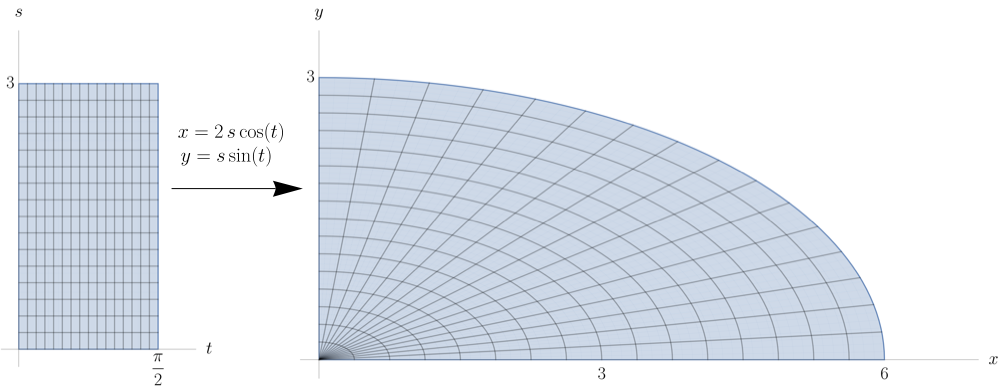
New coordinates (cont 2)
Even better, the function simplifies under the transformation:
$$\begin{align} 4-(x^2+4y^2) &= 4-\left((2s\cos(t))^2 + 4(s\sin(t))^2\right)\\ &=4-4s^2(\cos^2(t)+\sin^2(t)) = 4-4s^2. \end{align}$$Bringing us to:
$$\iint_{E} \left(4-(x^2+4y^2)\right) dA = \int_0^{2\pi} \int_0^1 (4-4s^2)\,\color{red}{?}\,ds\,dt.$$The last piece
The last piece of the puzzle is the $\color{red}?$ in
$$\int_0^{2\pi} \int_0^1 (4-4s^2)\,\color{red}{?}\,ds\,dt.$$It should be exactly analogous to the $\color{red}r$ in polar coordinates:
$$\int_{\alpha}^{\beta} \int_a^b F(r,\theta)\,\color{red}{r}\,dr\,d\theta.$$Last piece (cont)
Recall that the $r$ in the $r\,dr\,d\theta$ of polar coordinates accounts for the fact that a polar region doesn't break up evenly.
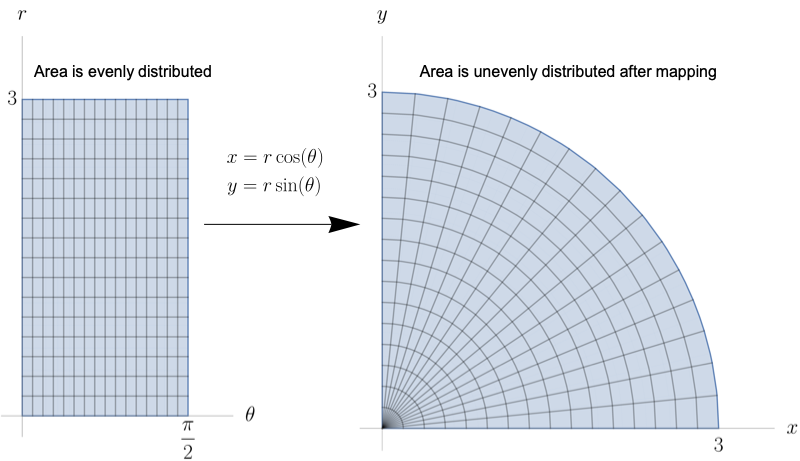
In the context of Change of Variables, this boils down to the fact that the mapping from one coordinate system to the other distorts area.
Last piece (cont 2)
Now, $x=2s\cos(t)$ and $y=s\sin(t)$.

Thus, we've stretched the image out twice as much in the $x$ direction so the area distortion is twice as much. Thus, perhaps
$$dA = 2s\,ds\,dt.$$Last piece (cont 3)
We can now finish off the integral:
$$\begin{align} \iint_{E} \left(4-(x^2+4y^2)\right) dA &= \int_0^{2\pi} \int_0^1 (4-4s^2)\,2s\,ds\,dt \\ &= 16\pi\int_0^1(s-s^3)\,ds = 4\pi. \end{align}$$The Jacobian
When we have a function (often called a transformation in this context) $T:\mathbb R^2\to\mathbb R^2$ there is a a standard tool called the Jacobian used to measure how it distorts area. Write $T$ componentwise:
$$T(s,t) = (x(s,t),y(s,t)), \text{ then}$$ $$JT = \left|\frac{\partial(x,y)}{\partial(s,t)}\right| = \left|\Big| \begin{matrix} \partial x/\partial s & \partial x/\partial t \\ \partial y/\partial s & \partial y/\partial t \end{matrix} \Big|\right|.$$That's a determinant inside an absolute value.
Jacobian example
Let's find the Jacobian for the general elliptic coordinates:
$$x = R_1\,s\,\cos(t) \: \text{ and } \: y = R_2\,s\sin(t).$$ $$\begin{align} \left|\frac{\partial(x,y)}{\partial(s,t)}\right| &= \left|\begin{matrix} R_1\cos(t) & -R_1\,s\,\sin(t) \\ R_2\sin(t) & R_2\,s\cos(t)\end{matrix} \right| \\ &= R_1R_2s\cos^2(t) + R_1R_2s\sin^2(t) = R_1R_2s. \end{align}$$This agrees with our prior example where $R_1=2$ and $R_2=1$.
Integrating over a parallelogram
Let $P$ denote the parallelogram bound by the lines
$$\begin{array}{cccc} 3x-y=0 & 3x-y=8 & 3y-x=0 & 3y-x=8 \end{array}$$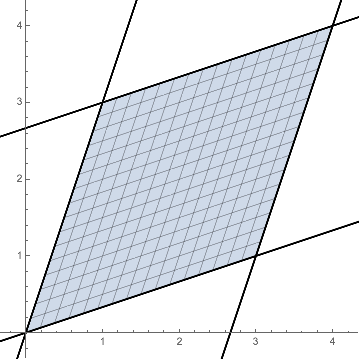
Parallelogram (cont)
We wish to set up a single, iterated integral representing
$$\iint_P xy\,dA.$$To do so, introduce $s$ and $t$ defined by
$$s = 3x-y \: \text{ and } \: t = 3y-x.$$For then, $0<s<8$ and $0<t<8$. Solving, we get
$$x = (3 s + t)/8 \: \text{ and } \: y = (s + 3 t)/8.$$Parallelogram (cont 2)
The Jacobian is
$$\left|\frac{\partial(x,y)}{\partial(s,t)}\right| = \left|\begin{matrix} 3/8 & 1/8 \\ 1/8 & 3/8\end{matrix} \right| = \frac{1}{8}. $$Thus, the integral is
$$\begin{align} \iint_{p} xy \, dA &= \frac{1}{8}\int_0^{8} \int_0^8 \frac{3s+t}{8}\frac{3t+s}{8}\,ds\,dt. \end{align}$$Plotting parametric regions
Sometimes it's up to you to find the parametric description of a region. This parametric plotter can help verify if you've got the right region.