Calc III Online Presentations
As we all know, a shifting reality has forced us to move to remote teaching for the rest of the semester. This web page complements our existing class web page and coordinates the online materials I'm developing to get us through this. You should also check out our revised syllabus.
The biggest addition to the course is a series of online presentations I'm developing to disseminate the material. These should be viewable in any reasonably new web browser or even on a tablet or smart phone. Please alert me to any difficulties as soon as you encounter them!
Note that the presentations linked on this page are asynchronous - i.e., you go through them at a time that works for you. In addition to the presentations, I'm planning on holding online office hours during the first half of our regularly scheduled class hours. I will email you a standing Google Meet link to access that.
Outline
-
Tuesday, March 24: Intro to the new tools
-
Overview
Today, we're going to ease back into the new reality by just getting acquainted with some of our new tools and going over the new expectations. Jump into the Presentation on presentations link below to get started.
- The Presentation presentation
-
Assignments
Again, the main goal for now is to acquaint ourselves with some new tools and to make sure that we can use the old remotely. To that end,
- Check out our revised syllabus
- Go through the Presentation presentation. Please let me know of any glitches that arise.
-
Overview
-
Thursday, March 26: Double Integrals
-
Overview
Today, we're going to get into some actual mathematics and talk about double integrals! This material is covered in sections 13.1 and 13.2 of our text.
- Presentation
-
Assignments
Recall that we'll be leaning a bit more heavily on online HWs for the remainder of your grade. As a result, this HW has a six problem worth 20 points.The first part of your homework is a MyOpenMath assignment. It's got five problems worth 3 points each. That's weighed a bit more heavily than some of our past MyOpenMath assignments but you login just the way you always have.In addition, you've got a five point, randomly generated forum question that you can answer by responding to this forum post. Your mission is to explain how to evaluate the double integral obtained by choosing your login name from the list below.The tentative due date for all this stuff is next Tuesday, March 31.
-
Overview
-
Tuesday, March 31: More general regions
-
Overview
Last time, we met the concept of a double integral, which is very cool but also fairly restrictive. It allows us to compute the volume under any function and over any rectangle. Today, we'll talk ways to compute the volume over shapes that might not be rectangles.
- Presentation
-
Assignments
First off, don't forget that there's a MyOpenMath assignment due tonight - March 31!In addition, there's another MyOpenMath due in one week - March 7. Generally, I'll make problems assigned one week due the following Tuesday.Finally, here are two more "discussion" problems of my own devising:Problem 1: Evaluate $$\iint_R xy \, dA$$ where $R$ is the region plotted here:
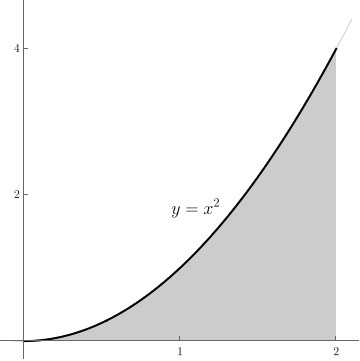 Problem 2: Evaluate $$\int_0^1 \int_y^1 \sin(x^2) \, dx \, dy.$$
Problem 2: Evaluate $$\int_0^1 \int_y^1 \sin(x^2) \, dx \, dy.$$
-
Overview
-
Thursday, April 2: Polar integrals
-
Overview
Today, we're going to talk about the use of integration in polar coordinates to simplify integration over regions that display circular symmetry. This is all section 13.3 of our text.
-
Presentation
-
New Features
Today's presentation has some new features:
- I've reduced the font-size across the whole document so that it should be more appropriate for viewing on your laptop, rather than from a projector.
- The slide show is now two-dimensional. I had made it linear for ease of use for folks who hadn't seen the software before. I really think that making two-dimensional is more natural to break up the presentation into parts, though.
- There's a menu button in the lower left to make it easier to navigate the document as a whole.
- You can push the 'b' button to pull up a chalkboard or the 'c' button to pull up a crayon to mark on an individual page. While not particularly useful for reading, my hope is that is should make it much easier for me to write down on the fly computations while going over it during a Google Meet.
-
New Features
-
Assignments
First off, I do expect quiz over the weekend. More on that via email soon.There's another MyOpenMath due next Tuesday, March 7. That makes two assignments due that day!.Finally, here's one more problem for you to try:Problem: Evaluate $$\iint_D \cos(x^2+y^2) \, dA$$ where $D$ is the disk of radius $\sqrt{\pi}$ centered at the origin.
-
Overview
-
Friday, April 3:
Quiz
There will be a 10 point quiz opening today. You can start it anytime between Friday, at 8:00 AM and finish anytime by Sunday at 11:59 PM. It will be time limited, though, so that you have 30 minutes to complete once you've started it.There will be two questions, both double integrals:
- One double integral will be over a rectangle
- The other double integral will be over a more general region
-
Tuesday, April 7: Change of variables
-
Overview
Today, we're going to push the polar coordinate stuff we did last time to talk about changes of variables to new coordinate systems more generally. This stuff is not really covered in our text so, hopefully, this will be a good presentation!
- Presentation
-
Assignments
- There's a MyOpenMath due next Tuesday, April 14,
- This forum question asks you to set up an integral over the parallelogram you get from this list:
-
There's the following two questions:
Problem 1: Use an elliptic change of variables to find the volume under the graph of $f(x,y)= 36 - (4 x^2 + 9 y^2)$ and over the $xy$-plane.Problem 2: Let $P$ denote the parallelogram defined by the inequalities $-1 \leq x + 2 y \leq 1$ and $-1 \leq x - 2 y \leq 1$. Set up a single iterated integral over a rectangle to represent $$\iint_P f(x,y) \,dA.$$
-
Overview
-
Thursday, April 9: Triple integrals
-
Overview
Today, we're going to move to triple integrals, which is also well covered in section 13.6 of our text
- Presentation
-
Assignments
The only HW for this section is a MyOpenMath due next Tuesday, April 14. That makes two assignments due that day!.
-
Overview
-
Tuesday, April 14: Cylindrical and spherical coordinates
-
Overview
Today, we jump into our penultimate topic - cylindrical and spherical coordinates. The presentation today focuses on cylindrical but we'll finish up the spherical stuff next time.
- Presentation
-
Assignments
There is a MyOpenMath on this material.
-
Overview
-
Wednesday, April 15:
Quiz
There will be a 10 point quiz opening today. You can start it anytime between Wednesday, at 5:00 AM and finish anytime by Friday at 11:59 PM. It will be time limited, though, so that you have 30 minutes to complete once you've started it.There will be two questions:
- One polar integral where you integrate over a disk or part of a disk
- One change of variables where you integrate over a parallelogram.
- Tuesday, April 21: Line integrals
-
Overview
Finally, we've reached our last topic for the semester - Line Integrals! This stuff is largely section 15.3 of our text.
- Presentation
-
Assignments
There is a MyOpenMath on this material.
-
Overview