Fun with ranking¶
Today, we're going to get our hands on some data so we can make predictions for one of the tournaments coming up this weekend.
Imports¶
First, we'll import some of the stuff we need.
import numpy as np
# A tool for getting data
import pandas as pd
# A sparse matrix representation
from scipy.sparse import dok_matrix
# An eigenvalue computer for sparse matrices
from scipy.sparse.linalg import eigs
Getting data¶
For this project we're going to use data currated by Ken Massey for his Massey Ratings project. I'll show you exactly how to grab this data in class but, for convenience, I've gone ahead and stored the relevant data on my web site. I also added some column headers so that we can work with the data as normal CSV files. You can grab the men's game data like so:
game_data = pd.read_csv(
'https://marksmath.org/data/MasseyData/mens2018/games_03062018.csv'
)
game_data.head()
Note that WTeamID and LTeamID refer to team IDs stored in the teams.csv file.
teams = pd.read_csv(
'https://marksmath.org/data/MasseyData/mens2018/teams.csv'
)
num_teams = teams.shape[0]
teams.tail()
If you want the data for women's season, just change the mens2018 to womens2018 in both URLs and re-execute.
Tweaking our formula¶
Recall that we are going to set up a matrix
$$M = \left(m_{ij}\right),$$where each $m_{ij}$ looks something like so:
$$aw \times \frac{ww \times w + sw \times s/t}{n^p}.$$Thus, your next step is to choose some values for the following parameters that you think are likely to help with your rankings. As set up currently, they should give exactly the basic eigen-rankings. You can fiddle with it a bit to see if there's any noticable effects on our predictions.
# The weight of a win
ww = 1
# The extra weight of an away win relative to a home win
aw = 1
# The weight of the score
sw = 0
# The exponent of $n$
p = 1
Compute the rankings!¶
The following code should just auto-compute the overall rankings in terms of what we've done so far.
# This might take a few moments.
games = [
{
'win_id':row['WTeamID'],
'win_score':int(row['WScore']),
'win_loc':row['WLoc'],
'lose_id':row['LTeamID'],
'lose_score':int(row['LScore'])
}
for (idx,row) in game_data.iterrows()
]
def num_games(team_id):
return len([game for game in games \
if game['win_id'] == team_id or game['lose_id'] == team_id])
M = dok_matrix((num_teams,num_teams))
for game in games:
win_team = game['win_id']
w_num_games = num_games(win_team)**p
win_score = int(game['win_score'])
lose_team = game['lose_id']
l_num_games = num_games(lose_team)**p
lose_score = int(game['lose_score'])
total_score = win_score+lose_score
if game['win_loc'] == 1:
whw = 1
lhw = aw
elif game['win_loc'] == -1:
whw = aw
lhw = 1
else:
whw = 1
lhw = 1
M[win_team-1,lose_team-1] = M[win_team-1,lose_team-1] + whw*ww/w_num_games + \
(whw*sw*win_score/total_score)/w_num_games
M[win_team-1,lose_team-1] = M[win_team-1,lose_team-1] + \
(lhw*sw*lose_score/total_score)/l_num_games
value, vector = eigs(M, which = 'LM', k=1)
vector = abs(np.ndarray.flatten(vector.real))
order = list(vector.argsort())
order.reverse()
ranking = [(vector[k],teams.iloc[k]['TeamName']) for k in order]
ranking[:10]
Simulate a tournament¶
Now, suppose we want to use these rankings to simulate a tournament. For example, here's what the recently completed men's Big South tournament looked like:
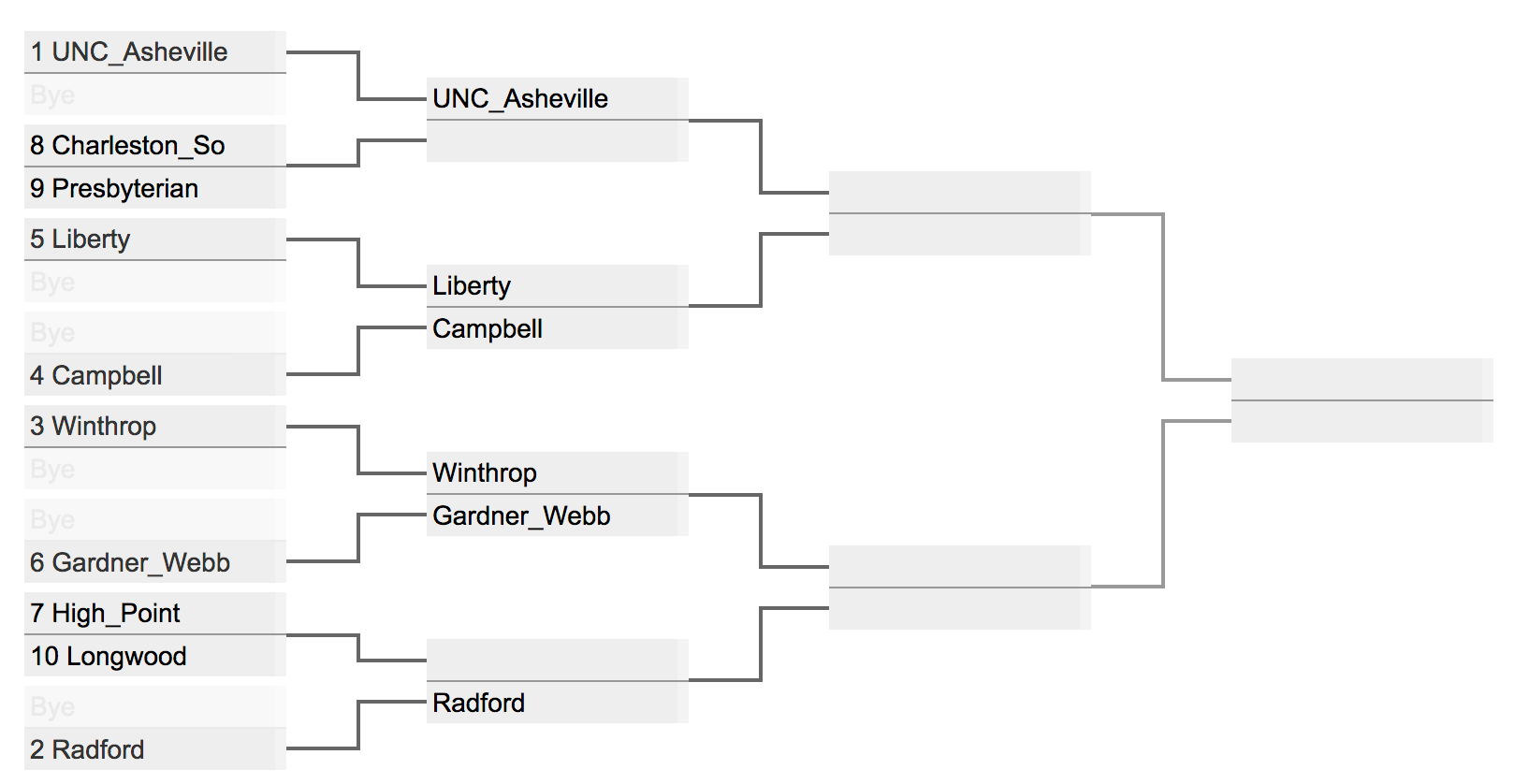
To simulate this tournament, we'll need a way to extract those teams from our big list of all teams and a way to represent the tournament itself. Unfortunately, the Massey data has no information on conferences so we'll just have to list the teams ourselves. Not too big a deal. Here's how to define the Big South and extract the teams in order of ranking:
big_south = [
'Campbell','Charleston_So','Gardner_Webb','High_Point','Liberty',
'Longwood','Presbyterian','Radford','UNC_Asheville','Winthrop'
]
ranked_big_south = [team for team in ranking if team[1] in big_south]
ranked_big_south
Now, it's pretty easy to just fill out your brackets with pencil and paper based on our rankings. If you really like basketball, you probably want to do that anyway. If we want to automate the procedure at all, we'll need to tell our program what the first round looks like. I suppose this is a reasonable representation:
round1 = [
'UNC_Asheville','Bye',
'Charleston_So','Presbyterian',
'Liberty','Bye',
'Bye','Campbell',
'Winthrop','Bye',
'Bye','Gardner_Webb',
'High_Point','Longwood',
'Bye','Radford'
]
Moving on from here involves a bit more programming that we really want to get into. Fortunately, there's a Javascript program that will generate the bracket based on this information for us. We've just got to generate query string that the program understands:
def get_strength(team):
if team == "Bye":
return 0
else:
idx = [ranked_team[1] for ranked_team in ranked_big_south].index(team)
return ranked_big_south[idx][0]
ratings = [get_strength(team) for team in round1]
q = "?"
for k in range(len(round1)):
q = q + 'team=' + round1[k] + '&'
q = q + 'rating=' + str(get_strength(round1[k]))
if k<len(round1)-1:
q = q + '&'
q
Check it out!!:
import webbrowser
webbrowser.open(
'https://marksmath.org/visualization/eigenbrackets/tourney_from_rankings.html' + q
)
Exercise 1¶
Generate an eigenbracket for the women's Big South Tournament that starts tomorrow. You can view the initial brackets on this Wikipedia page. Be sure to read in the correct data by making the two small edits necessary at the top of this page.
Exercise 2¶
Generate an eigenbracket for the men's ACC Tournament that's going on right now! As of this morning, the current state of the bracket looks like so:
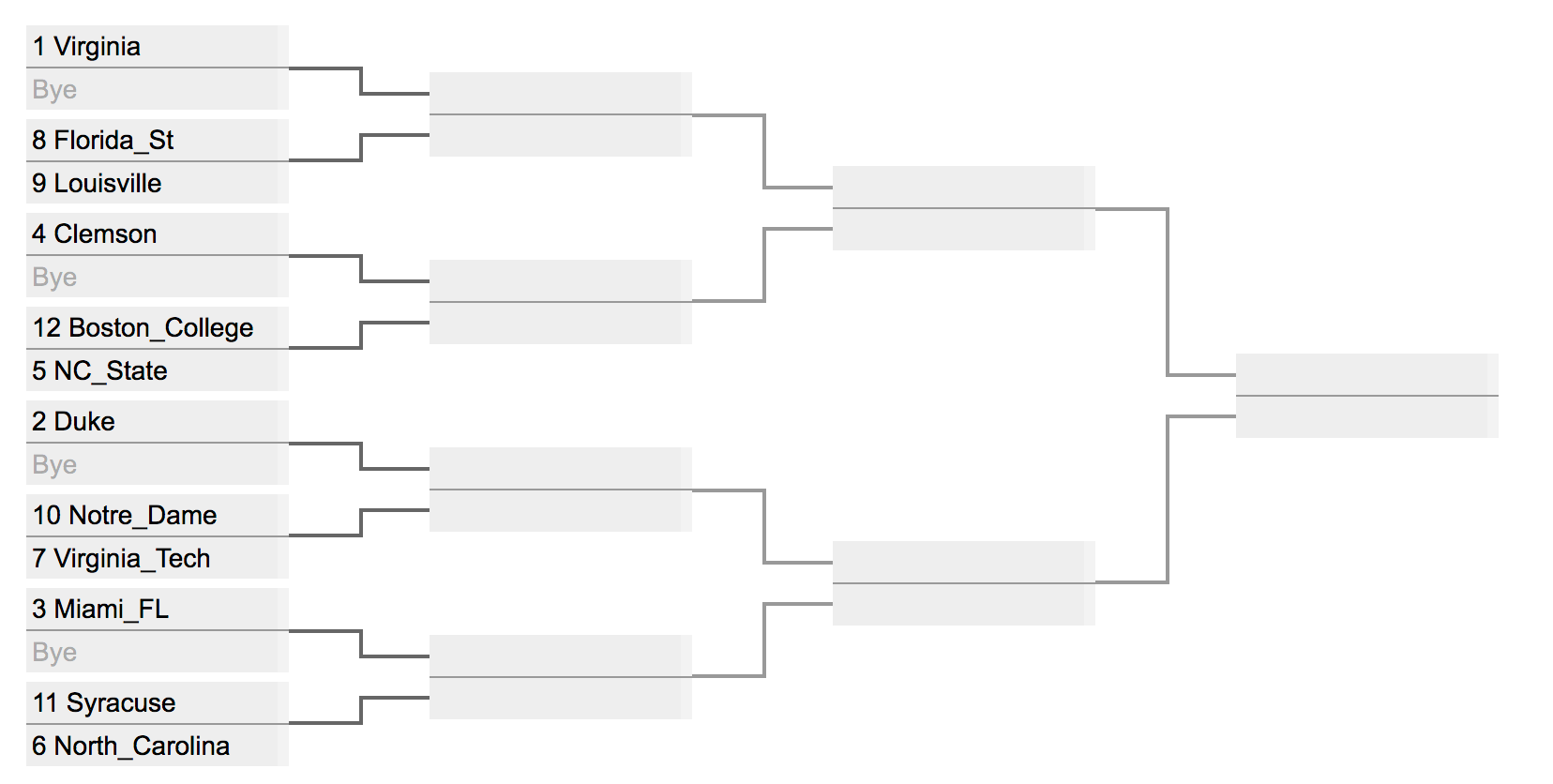
For your convenience, the teams in the ACC as listed in the Massey data are as follows:
acc = [
'Boston_College','Clemson','Duke','Florida_St','Georgia_Tech',
'Louisville','Miami_FL','NC_State','North_Carolina','Notre_Dame',
'Pittsburgh','Syracuse','Virginia','Virginia_Tech','Wake_Forest'
]
Exercise 3¶
Generate the brackets for the Men's or Women's NCAA Tournament. Be sure to submit to ESPN!!