The bifurcation diagram

Subsection 2.6.1 The bifurcation diagram

A fabulous illustration of the types of behavior that can arise in a family of functions indexed by a single parameter and each with a single critical point can be generated as follows: For each value of the parameter, compute a large number points of the orbit of the critical point (maybe 1000 iterates). Since we're interested in long term behavior, rather than any transient behavior, discard the first few iterates (maybe 100). Then, plot the remaining points in a vertical column at the horizontal position indicated by the parameter.

The orbit of a critical point is called a critical orbit and its importance is due to the following theorem.

Theorem 2.25.

If \(f:\mathbb C \to \mathbb C\) has an attractive or super-attractive orbit, then that orbit must attract at least one critical point.

Note that this is really a theorem of complex dynamics. There is an analogous statement for real dynamics but it's a bit more complicated and its proof takes us a bit farther astray than we want. This is a great example of complex analysis being, in some ways, more elegant than real analysis.

Regardless, the theorem has important implications for real iteration. For example, a polynomial of degree \(n\) can have at most \(n-1\) attractive orbits. Furthermore, if all the critical points happen to be real, we can find all the attractive behavior by simply iterating from the critical points. If we do this systematically for the quadratic family, plotting the columns to generate the bifurcation diagram, we get Figure 2.26

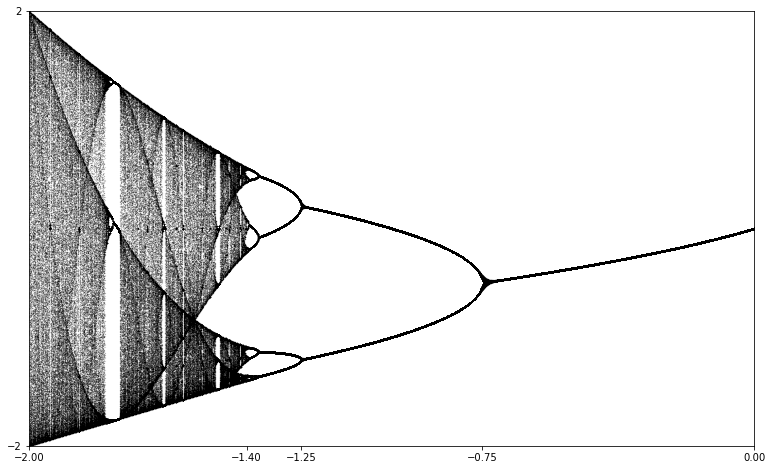
Figure 2.26. The bifurcation diagram for the quadratic family

We can interpret this diagram as follows:

For \(-0.75 < c < 0\text{,}\) there is an attractive fixed point.
For \(-1.25 < c < -0.75\text{,}\) there is an attractive orbit of period \(2\text{.}\)
As \(c\) passes from just above \(-0.75\) to just below \(-0.75\text{,}\) the dynamics of \(f_c\) undergo a bifurcation.
For \(c\) just a little less than \(-1.25\text{,}\) there is an attractive orbit of period four. This orbit bifurcates soon into an attractive orbit of period 8. It appears that this behavior continues as \(c\) decreases.
For \(c\) somewhere around \(c\approx -1.4\text{,}\) the period doubling appears to stop and we get more complicated behavior.

Generally, a bifurcation occurs at a parameter value \(c=c_0\) if the global dynamical behavior of the function \(f_c\) undergoes some qualitative change as \(c\) passes through \(c_0\text{.}\) There are number of different types of bifurcations that can occur, depending on the nature of the qualitative behavior under consideration. The bifurcations that are evident in Figure 2.26 in the range \(-1.4 < c < 0\) are called period doubling bifurcations.